
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).
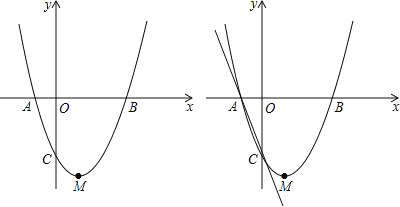
(1)求该抛物线的解析式及顶点M坐标;
(2)求△BCM面积与△ABC面积的比;
(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3=(x﹣1)2﹣4,M(1,﹣4).(2)S△BCM:S△ABC=3:6=1:2.(3)Q点为(2,﹣3)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)
,3)
【解析】
试题分析:(1)有抛物线与x轴交于点A(﹣1,0),B(3,0)两点,则可设抛物线解析式为y=a(x+1)(x﹣3).由与y轴交于点C(0,﹣3),则代入易得解析式,顶点易知.
(2)求△BCM面积与△ABC面积的比,由两三角形不为同高或同底,所以考虑求解求出两三角形面积再作比即可.因为S△BCM=S梯形OCMD+S△BMD﹣S△BOC,S△ABC=![]() ABOC,则结论易得.
ABOC,则结论易得.
(3)由四边形为平行四边形,则对边PQ、AC平行且相等,过Q点作x轴的垂线易得Q到x轴的距离=OC=3,又(1)得抛物线解析式,代入即得Q点横坐标,则Q点可求.
解:(1)设抛物线解析式为y=a(x+1)(x﹣3),
∵抛物线过点(0,﹣3),
∴﹣3=a(0+1)(0﹣3),
∴a=1,
∴抛物线解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴M(1,﹣4).
(2)如图1,连接BC、BM、CM,作MD⊥x轴于D,
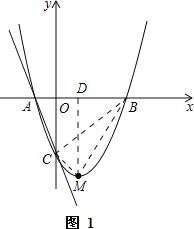
∵S△BCM=S梯形OCMD+S△BMD﹣S△BOC
=![]() (3+4)1+
(3+4)1+![]() 2×4﹣
2×4﹣![]() 33
33
=![]() +
+![]() ﹣
﹣![]() =3
=3
S△ABC=![]() ABOC=
ABOC=![]() 43=6,
43=6,
∴S△BCM:S△ABC=3:6=1:2.
(3)存在,理由如下:
①如图2,当Q在x轴下方时,作QE⊥x轴于E,
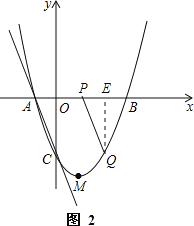
∵四边形ACQP为平行四边形,
∴PQ平行且相等AC,
∴△PEQ≌△AOC,
∴EQ=OC=3,
∴﹣3=x2﹣2x﹣3,
解得 x=2或x=0(与C点重合,舍去),
∴Q(2,﹣3).
②如图3,当Q在x轴上方时,作QF⊥x轴于F,

∵四边形ACPQ为平行四边形,
∴QP平行且相等AC,
∴△PFQ≌△AOC,
∴FQ=OC=3,
∴3=x2﹣2x﹣3,
解得 x=1+![]() 或x=1﹣
或x=1﹣![]() ,
,
∴Q(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3).
,3).
综上所述,Q点为(2,﹣3)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)
,3)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知张强家、体育场、文具店在同一直线上,下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中![]() 表示时间,
表示时间,![]() 表示张强离家的距离.
表示张强离家的距离.

根据图象解答下列问题:
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)求张强从文具店回家过程中![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )

A. 逐渐增加 B. 逐渐减小
C. 保持不变且与EF的长度相等 D. 保持不变且与AB的长度相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图(图1,图2).请你根据图中提供的信息,解答以下问题:

(1)该班共有 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为 ;
(4)若全校有2000名学生,则“其他”部分的学生人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发兼零售的文具店规定:凡一次购买铅笔300枝以上,(不包括300枝),可以按批发价付款,购买300枝以下,(包括300枝)只能按零售价付款。小明来该店购买铅笔,如果给八年级学生每人购买1枝,那么只能按零售价付款,需用120元,如果购买60枝,那么可以按批发价付款,同样需要120元,
(1) 这个八年级的学生总数在什么范围内?
(2) 若按批发价购买6枝与按零售价购买5枝的款相同,那么这个学校八年级学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
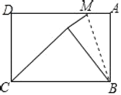
【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
(1)若CF交⊙O于点G,⊙O的半径是4,求![]() 的长;
的长;
(2)请判断直线BF与⊙O的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的方格(每小格边长为1)内有1只甲虫A,它爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(﹣1,﹣4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息.

(1)图中B→D( , ),C→ (+1, );
(2)若甲虫A的爬行路线为A→B→C→D,计算甲虫A爬行的路程?
(3)若甲虫A的爬行路线依次为(+2,+3),(﹣2,+1),(+3,﹣5),(﹣4,+2),最终到达点P处,请在图中标出甲虫A的爬行路线示意图及最终点P的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com