
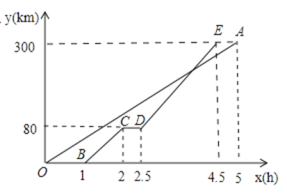
����Ŀ���ס����������300km��һ��������һ���γ��Ⱥ�Ӽس���ʻ���ҵء���ͼ���߶�OA��ʾ������صľ���![]() ��km����ʱ��
��km����ʱ��![]() ��h��֮��ĺ�����ϵ������BCDE��ʽ�γ���صľ���
��h��֮��ĺ�����ϵ������BCDE��ʽ�γ���صľ���![]() ��km����ʱ��
��km����ʱ��![]() ��h��֮��ĺ�����ϵ������ͼ����������⣺
��h��֮��ĺ�����ϵ������ͼ����������⣺
��1���߶�CD��ʾ�γ���;��ͣ���� h.
��2�����߶�DE��Ӧ�ĺ�����ϵʽ��2.5��x��4.5��.
��3����γ��Ӽس������ʱ���ϻ���.
���𰸡���1��0.5����2��![]() ����3��2.9
����3��2.9
��������
��1������ͼ��ó�CD���ʱ��Ϊ2.5-2=0.5���ó��𰸼��ɣ�
��2������D������Ϊ����2.5��80����E������Ϊ����4.5��300���������������ʽ���ɣ�
��3������OA�Ľ���ʽ�ó�����60x=110x-195ʱ����������γ��ϻ�����ʱ�䣮
�⣺��1������ͼ��ɵã��߶�CD��ʾ�γ���;��ͣ���ˣ�2.5-2=0.5Сʱ��
��2������D����������2.5��80����E����������4.5��300����
����y=kx+b���ã�![]() ��
��
��ã�![]() ��
��
���߶�DE��Ӧ�ĺ�������ʽΪ��y=110x-195��2.5��x��4.5����
��3����A����������5��300����
�������ʽy=ax�ã�
300=5a��
��ã�a=60��
��y=60x����60x=110x-195��
��ã�x=3.9����3.9-1=2.9��Сʱ����
�𣺽γ��Ӽس�����2.9Сʱ�ϻ�����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�����κ���a������[a]��ʾ������a�����������
���磺[5.7]=5��[5]=5��[��1.5]=��2��
��1��[��![]() ]=�� ����
]=�� ����
��2�����[a]=3����ôa��ȡֵ��Χ���� ����
��3�����[![]() ]=��3����������������������x��
]=��3����������������������x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����3��A�ͳ���2��B�ͳ���������һ�ο��˻���19�֣���2��A�ͳ���3��B�ͳ���������һ�ο��˻���21�֣�
��1��1��A�ͳ���1��B�ͳ�����������һ�ηֱ�����˻����ٶ�?
��2��ij������˾����49�ֻ���ƻ�ͬʱ����A�ͳ�![]() ����B�ͳ�
����B�ͳ�![]() ����һ�����꣬��ǡ��ÿ�������������
����һ�����꣬��ǡ��ÿ�������������
����![]() ��
��![]() ��ֵ��
��ֵ��
����A�ͳ�ÿ�������130Ԫ/����B�ͳ�ÿ�������200Ԫ/�������������������Ƕ���Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ǰ尴��ͼ��ʾ�ķ�ʽ���ã������н����в���ȷ����( )
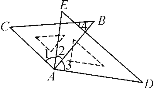
A. ��1����3 B. �����2��30��������AC��DE
C. �����2��30��������BC��AD D. �����2��30��������4����C
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y= ![]() x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0����
x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0����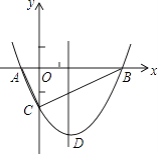
��1���������ߵĽ���ʽ������D�����ꣻ
��2���жϡ�ABC����״��֤����Ľ��ۣ�
��3����M�������߶Գ����ϵ�һ�����㣬����ACM�ܳ���Сʱ�����M�����꼰��ACM����С�ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ�DF��AB������ΪF��DE��DG����ADG����AED������ֱ�Ϊ50��25������EDF�����Ϊ(����)

A. 35B. 25C. 15D. 12.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������DEF�У�DE��DF����B��EF���ϣ��ҡ�EBD��60�㣬C������BD�ϵ�һ������(�����B�غϣ���BC��BE)��������BE�Ͻ�ȡBA��BC������AC��
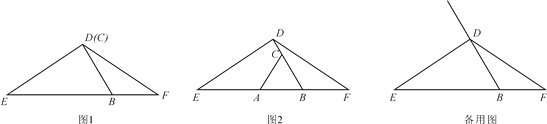
��1������C���߶�BD��ʱ��
������C���D�غϣ���������ⲹȫͼ1����ֱ��д���߶�AE��BF��������ϵΪ________��
����ͼ2������C�����D�غϣ���֤��AE��BF��CD��
��2������C���߶�BD���ӳ�����ʱ���õ�ʽ��ʾ�߶�AE��BF��CD֮���������ϵ������֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com