
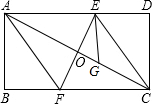
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE;过点E作EG⊥AD交AC于点G.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE;过点E作EG⊥AD交AC于点G.分析 (1)当顶点A与C重合时,折痕EF垂直平分AC,由OA=OC,得∠AOE=∠COF=90°,由题意得AD∥BC,∠EAO=∠FCO,可证明△AOE≌△COF,从而得出∴四边形AFCE是菱形.
(2)由EG⊥AD,得∠AEG=90°,可证明△AOE∽△AEG,写出比例式$\frac{AE}{AG}$=$\frac{AO}{AE}$,即可得出AE2=AO•AG,即2AF2=AC•AG;
(3)根据四边形AFCE是菱形,得出AF=AE=8,在Rt△ABF中,利用勾股定理得AB2+BF2=AF2,AB2+BF2=82,即可得出(AB+BF)2-2AB•BF=a2①,根据△ABF的面积为b,可求得AB•BF=2b②,再由①、②得:(AB+BF)2=a2+4b,得出AB+BF=$\frac{7}{5}$a,设DE=x,则CD=($\frac{7}{5}$a-x),根据三角形面积公式可得DE,再根据余角的性质和正切的定义即可求解.
解答 (1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
在△AOE与△COF中,
$\left\{\begin{array}{l}{∠AOE=∠COF}\\{OA=OC}\\{∠EAO=∠FCO}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AFCE是菱形.
(2)证明:∵EG⊥AD
∴∠AEG=90°,
∵∠AOE=90°,
∴∠AEG=∠AOE,
∵∠EAO=∠EAG,
∴△AOE∽△AEG,
∴$\frac{AE}{AG}$=$\frac{AO}{AE}$,
∴AE2=AO•AG,即2AF2=AC•AG; (3)解:∵四边形AFCE是菱形,
(3)解:∵四边形AFCE是菱形,
∴AF=AE=a,
在Rt△ABF中,AB2+BF2=AF2,
∴AB2+BF2=a2,
∴(AB+BF)2-2AB•BF=a2①,
∵△ABF的面积为b,
∴$\frac{1}{2}$AB•BF=b,
∴AB•BF=2b②,
由①、②得:(AB+BF)2=a2+4b,
∵AB+BF>0,
∴AB+BF=$\sqrt{{a}^{2}+4b}$=$\frac{7}{5}$a,
设DE=x,则CD=($\frac{7}{5}$a-x),则
$\frac{1}{2}$x($\frac{7}{5}$a-x)=b=$\frac{6{a}^{2}}{25}$,
解得x1=$\frac{3}{5}$a,x2=$\frac{4}{5}$a(舍去),
∴CD=$\frac{4}{5}$a,
∵∠EAG+∠EGA=∠OEG+∠EGA=90°,
∴∠EAG=∠OEG,
∴tan∠OEG=tan∠EAG=$\frac{CD}{AD}$=$\frac{\frac{4}{5}a}{a+\frac{3}{5}a}$=$\frac{1}{2}$.
点评 本题考查了相似形综合题,涉及菱形的判定和性质、勾股定理、矩形的性质以及相似三角形的判定和性质的知识点,综合性极强,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
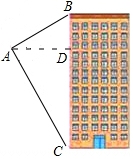 如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )
如图,热气球从空中的A处看一栋楼的顶部仰角为30°,看这栋楼的俯角为60°.热气球与楼的水平距离为120m.这栋楼的高度为( )| A. | 160m | B. | 160$\sqrt{3}$m | C. | (160-160$\sqrt{3}$)m | D. | 360m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com