
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2)延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x 轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为_____.

【答案】5×(![]() )2017.
)2017.
【解析】
根据勾股定理求出AB,证明△ABA1∽△DOA,根据相似三角形的性质求出A1B,计算求出A1C,根据正方形的面积公式求出正方形A1B1C1C的面积,总结规律,根据规律计算即可.
∵点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,
∵∠AOD=90°,
∴AB=AD=![]() =
=![]() ,∠ODA+∠OAD=90°,
,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,S正方形ABCD=5,
∴∠ABA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴Rt△ABA1∽Rt△DOA,
∴![]() ,即
,即![]() ,
,
解得,A1B=![]() ,
,
∴A1C=![]() ,
,
则正方形A1B1C1C的面积=(![]() )2=5×
)2=5×![]() ,
,
同理,正方形A2B2C2C1的面积=5×(![]() )2,
)2,
…
则第2018个正方形的面积为5×(![]() )2017,
)2017,
故答案为:5×(![]() )2017.
)2017.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
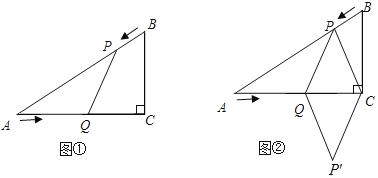
【题目】已知:如图①,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形, ![]() 是一个格点三角形.
是一个格点三角形.
![]() 在图
在图![]() 中,请判断
中,请判断![]() 与
与![]() 是否相似,并说明理由;
是否相似,并说明理由;
![]() 在图
在图![]() 中,以O为位似中心,再画一个格点三角形,使它与
中,以O为位似中心,再画一个格点三角形,使它与![]() 的位似比为2:1
的位似比为2:1
![]() 在图
在图![]() 中,请画出所有满足条件的格点三角形,它与
中,请画出所有满足条件的格点三角形,它与![]() 相似,且有一条公共边和一个公共角.
相似,且有一条公共边和一个公共角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.

(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
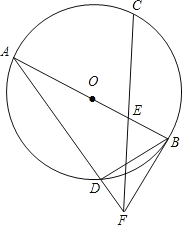
【题目】如图,AB是⊙O的直径,![]() ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
(1)求证:直线BF是⊙O的切线;
(2)若OB=2,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
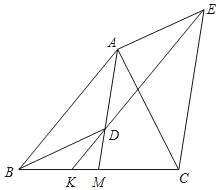
【题目】如图,AM是△ABC的中线,点D是线段AM上一点(不与点A重合).过点D作KD∥AB,交BC于点K,过点C作CE∥AM,交KD的延长线于点E,连接AE、BD.
(1)求证:△ABM∽△EKC;
(2)求证:ABCK=EKCM;
(3)判断线段BD、AE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
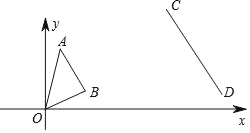
A. (0,0) B. (3,4)或(﹣6,2)
C. (5,3)或(-7,1) D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=﹣x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(﹣1,5),点A与y1的顶点B的距离是4.
(1)求y1的解析式;
(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )
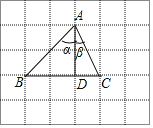
A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com