
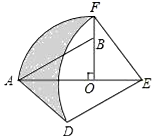
 如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )| A. | π | B. | π+5 | C. | $\frac{14-π}{4}$ | D. | $\frac{10-π}{4}$ |
分析 作DH⊥AE于H,根据勾股定理求出AB,根据阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积、利用扇形面积公式计算即可.
解答 解: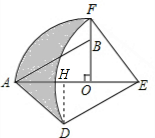 作DH⊥AE于H,
作DH⊥AE于H,
∵∠AOB=90°,OA=2,OB=1,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{5}$,
由旋转的性质可知,OE=OB=1,DE=EF=AB=$\sqrt{5}$,△DHE≌△BOA,
∴DH=OB=1,
阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积
=$\frac{1}{2}$×3×1+$\frac{1}{2}$×1×2+$\frac{90•π×{2}^{2}}{360}$-$\frac{90•π×5}{360}$
=$\frac{5}{2}$-$\frac{1}{4}$π,
故选:D.
点评 本题考查的是扇形面积的计算、旋转的性质、全等三角形的性质,掌握扇形的面积公式和旋转的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
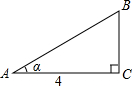 如图,已知在Rt△ABC中,∠C=90°,若AC=4,∠A=α,则BC的长为( )
如图,已知在Rt△ABC中,∠C=90°,若AC=4,∠A=α,则BC的长为( )| A. | BC=4sinα | B. | BC=$\frac{4}{cosα}$ | C. | BC=$\frac{4}{tanα}$ | D. | BC=4tanα |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
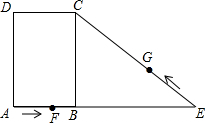 在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.
在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 要了解我市九年级学生的身高,应采用普查的方式 | |
| B. | 若甲队成绩的方差为5,乙队成绩的方差为3,则甲队成绩不如乙队成绩稳定 | |
| C. | 如果明天下雨的概率是99%,那么明天一定会下雨 | |
| D. | 一组数据4,6,7,6,7,8,9的中位数和众数都是6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a+3b=5ab | B. | (-a2)3=a6 | C. | (a+b)2=a2+b2 | D. | $\sqrt{8}-2\sqrt{2}=0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com