【题目】某电信公司手机的通讯卡有
，
两种业务类型：类卡收费标准是：不管通话时间多长，每部手机每月必须缴月租费12元，另外，通话费按0．2元/分钟计；类卡收费标准是：没有月租，但通话费按0．25元/分钟计．如图所示，是每月应缴费用
（元）与通话时间
（分钟）之间的函数图象．下列结论：
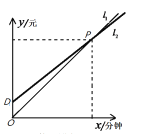
①图中
是类卡的收费方式所表示的函数图象；
②若李海本月的通话时间为180分钟，则他选择类卡省钱；
③若本月李海预缴了100元的话费，则他选择类卡划算；
④若类卡比类卡的话费多10元，则类卡和类卡的通话时间都是40分钟或类卡比类卡的通话时间多40分钟且类卡和类卡的通话时间分别为240分钟和200分钟．其中正确的结论有（ ）
A.①②③④B.②③④C.②③D.②④
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB=90°，AB=10cm，BC=6cm，若点P从点A出发，以每秒4cm的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．
（1）若点P在AC上，且满足△BCP的周长为14cm，求此时t的值；
（2）若点P在∠BAC的平分线上，求此时t的值；
（3）在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（阅读材料）
对于二次三项式
可以直接分解为
的形式，但对于二次三项式
，就不能直接用公式了，我们可以在二次三项式中先加上一项
，使其成为完全平方式，再减去这项，(这里也可把
拆成
与
的和)，使整个式子的值不变．
于是有：
，
我们把像这样将二次三项式分解因式的方法叫做添(拆)项法．
（应用材料）
上式中添(拆)项后先把完全平方式组合在一起，然后用______法实现分解因式．
请你根据材料中提供的因式分解的方法，将下面的多项式分解因式：
；
查看答案和解析>>
科目：初中数学 来源： 题型：
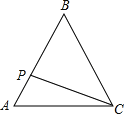
【题目】如图，正△ABC的边长为3cm,动点P从点A出发，以每秒1cm的速度，沿
的方向运动，到达点C时停止，设运动时间为x（秒），
,则y关于x的函数的图像大致为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
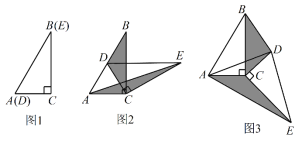
【题目】如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．
(1)操作发现：如图2，固定△ABC，使△DEC绕点C顺时针旋转．当点D恰好落在AB边上时，填空：
①线段DE与AC的位置关系是 ；
②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是 ；
(2)猜想论证：
当△DEC绕点C旋转到图3所示的位置时，小明猜想(1)中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小明的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知E是平行四边形ABCD中DA边的延长线上一点，且AE=AD，连接EC分别交AB，BE于点F、G．
（1）求证：BF=AF；
（2）若BD=12cm，求DG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又 去早餐店吃早餐，然后散步走回家，其中 x 表示时间，y 表示张强离家的距离。根据图象提供的信息，以下四个说法错误的是（ ）
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目：初中数学 来源： 题型：
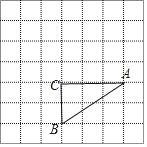
【题目】如图在7×7的正方形网格中，△ABC的顶点都在边长为1的小正方形的顶点上．
（1）将△ABC绕点B逆时针旋转90°，画出旋转后得到的△A1BC1；
（2）求出旋转过程中，线段BA扫过的图形的面积（结果保留π）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
