
分析 (1)首先把方程整理成一元二次方程的一般式,然后利用因式分解法解方程即可;
(2)首先把方程整理成一元二次方程的一般式,然后利用求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$进行计算即可.
解答 解:(1)(x-2)(x-3)=12,
整理得:x2-5x-6=0,
(x-6)(x+1)=0,
则x-6=0,x+1=0,
解得:x1=-1;x2=6;
(2)3y2-2$\sqrt{3}$y+1=0,
∵a=3,b=-2$\sqrt{3}$,c=1,
∴△=b2-4ac=12-12=0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2\sqrt{3}±0}{6}$=$\frac{\sqrt{3}}{3}$,
∴y1=y2=$\frac{{\sqrt{3}}}{3}$.
点评 此题主要考查了一元二次方程的解法,关键是掌握因式分解法和公式法解方程的步骤.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
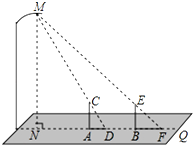 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小军正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小聪正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高BE为1.74米,MN⊥NQ,AC⊥NQ,BE⊥NQ,请你根据以上信息,求出小军身高AC的长(结果精确到0.01米)
晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小军正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小聪正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高BE为1.74米,MN⊥NQ,AC⊥NQ,BE⊥NQ,请你根据以上信息,求出小军身高AC的长(结果精确到0.01米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | BC=B'C' | B. | ∠A=∠A' | C. | AC=A'C' | D. | ∠C=∠C' |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com