
【题目】如图所示,在平面直角坐标系xOy中,B , C两点的坐标分别为 ![]() ,
, ![]() ,CD⊥y轴于点D , 直线l 经过点D.
,CD⊥y轴于点D , 直线l 经过点D.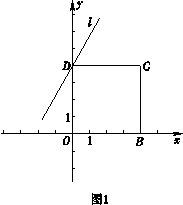
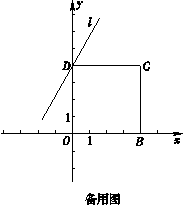
(1)直接写出点D的坐标;
(2)作CE⊥直线l于点E , 将直线CE绕点C逆时针旋转45°,交直线l于点F , 连接BF.
①依题意补全图形;
②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;
③通过思考、讨论,同学们形成了证明该猜想的几种思路:
思路1:作CM⊥CF , 交直线l于点M , 可证△CBF≌△CDM , 进而可以得出 ![]() ,从而证明结论.
,从而证明结论.
思路2:作BN⊥CE , 交直线CE于点N , 可证△BCN≌△CDE , 进而证明四边形BFEN为矩形,从而证明结论.
……
请你参考上面的思路完成证明过程.(一种方法即可)
【答案】
(1)
解: ![]()
(2)
解:①补全图形见图7.
②BF⊥直线l.
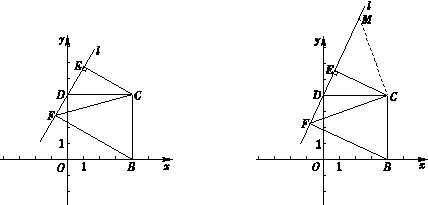
③法1:
证明:如图8,作CM⊥CF,交直线l于点M.
∵ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
∵ CE⊥直线l,CM⊥CF, ![]() ,
,
可得△CEF,△CEM 为等腰直角三角形, ![]() ,
,
CF=CM ①
∵ ![]() ,
, ![]() ,
,
∴ ∠BCF=∠DCM ②
又∵CB=CD, ③
∴ △CBF≌△CDM.
∴ ![]()
∴ ![]() .
.
∴ BF⊥直线l.
法2:
证明:如图9,作BN⊥CE,交直线CE于点N.
∵ ![]() ,
, ![]() ,
, ![]() ,
,

∴ ![]() ,
, ![]() .
.
∵ CE⊥直线l, BN⊥CE,
∴ ∠BNC=∠CED=90° ①
∴ ![]() ,
, ![]() .
.
∴ ∠1=∠2 . ②
又∵CB=CD, ③
∴ △BCN≌△CDE.
∴ BN= CE.
又∵ ![]() ,
,
可得△CEF为等腰直角三角形,EF = CE.
∴ BN= EF.
又∵ ![]() ,
,
∴ BN∥FE.
∴ 四边形BFEN为平行四边形.
又∵ ![]() ,
,
∴ 平行四边形BFEN为矩形.
∴ ![]() .
.
∴ BF⊥直线l
【解析】(1)由图可以直接得出D点坐标.
(2)③法1:如图8,作CM⊥CF , 交直线l于点M .
由 B(4,0) , C(4,4) , D(0,4) ,可得△CEF,△CEM 为等腰直角三角形, 由等腰三角形性质和已知条件证△CBF≌△CDM.由全等三角形的性质
BF⊥直线l.
【考点精析】利用等腰直角三角形和余角和补角的特征对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;互余、互补是指两个角的数量关系,与两个角的位置无关.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数),如北京时间的上午10:00时,东京时间的10点已过去了1小时,现在已是10+1=11:00.

(1)如果现在是北京时间8:00,那么现在的纽约时间是多少;
(2)此时(北京时间8:00)小明想给远在巴黎姑妈打电话,你认为合适吗?为什么?
(3)如果现在是芝加哥时间上午6:00,那么现在北京时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有4个红球、5个白球、11个黄球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取走若干个黄球,并放入相同数量的红球,搅拌均匀后,要使从袋中摸出一个球是红球的概率不小于![]() ,问至少需取走多少个黄球?
,问至少需取走多少个黄球?
查看答案和解析>>
科目:初中数学 来源: 题型:
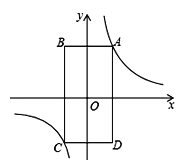
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
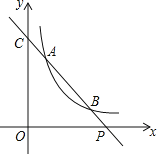
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国倡导“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口约为44亿人,数据44亿用科学记数法表示为( )
A. 44×108 B. 4.4×109 C. 4.4×108 D. 44×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
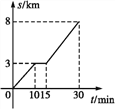
【题目】小明家距离学校8 km,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)小明修车前、后的行驶速度各是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com