
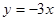 ②
②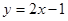 ③
③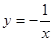 ④
④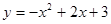 ,当x<0时其中
,当x<0时其中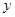 的值随
的值随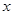 值的增大而增大的函数有( )
值的增大而增大的函数有( )| A.4个 | B.3个 | C.2个 | D.1个 |
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:不详 题型:解答题
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车装载量(吨) | 6 | 5 | 4 |
| 每吨所需运费(元/吨) | 120 | 160 | 100 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的解析式为
的解析式为 ,交
,交 、
、 轴分别于
轴分别于 、
、 两点,点
两点,点 在直线
在直线 上,
上, 为原点
为原点
 在
在 轴的负半轴上,且∠
轴的负半轴上,且∠ ,则
,则 ▲ ;
▲ ;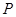 在
在 轴上,线段
轴上,线段 绕点
绕点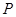 旋转
旋转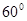 得到线段
得到线段 ,
, 恰好在直线
恰好在直线 上,则点
上,则点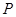 的坐标为 ▲ .
的坐标为 ▲ .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点
,点 在
在 正半轴上,且
正半轴上,且 .动点
.动点 在线段
在线段 上从点
上从点 向点
向点 以每秒
以每秒 个单位的速度运动,设运动时间为秒.点M、N在
个单位的速度运动,设运动时间为秒.点M、N在 轴上,且
轴上,且 是等边三角形.
是等边三角形. 的边长(用的代数式表示),并求出当等边
的边长(用的代数式表示),并求出当等边 的顶点
的顶点 运动到与原点
运动到与原点 重合时的值;
重合时的值; 的中点
的中点 ,以
,以 为边在
为边在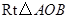 内部作如图2所示的矩形
内部作如图2所示的矩形 ,点
,点 在线段
在线段 上.设等边
上.设等边 和矩形
和矩形 重叠部分的面积为
重叠部分的面积为 ,请求出当
,请求出当 秒时,
秒时, 与的函数关系式,并求出
与的函数关系式,并求出 的最大值.
的最大值.



查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a元 |
| 超过3km的部分 | 每公里2.1元 | 每公里b元 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 元,两项优惠共
元,两项优惠共 元,请写出
元,请写出 关于
关于 的函数关系式;这时,政府最多需付出补贴资金多少元?
的函数关系式;这时,政府最多需付出补贴资金多少元?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 ,C种票张数为
,C种票张数为 .
. 与
与 之间的函数关系式;
之间的函数关系式; 元,求出
元,求出 (元)与
(元)与 (张)之间的函数关系式;
(张)之间的函数关系式;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com