
【题目】我们约定,在平面直角坐标系中两条抛物线有且只有一个交点时,我们称这两条抛物线为“郡园牵手抛物线”,这个交点为“郡园点”.例如:抛物线![]() 与
与![]() 是“郡园牵手抛物线”,“郡园点”为
是“郡园牵手抛物线”,“郡园点”为![]() .
.
(1)如图,若抛物线![]() 与
与![]() 为“郡园牵手抛物线”,求
为“郡园牵手抛物线”,求![]() 的值;
的值;
(2)在(1)的条件下,若点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的动点,过
上的动点,过![]() 作
作![]() 轴,
轴,![]() 为垂足,求
为垂足,求![]() 的最大值;
的最大值;
(3)在(1)的条件下,设点![]() 是抛物线
是抛物线![]() 与
与![]() 的“郡园点”,点
的“郡园点”,点![]() 是抛物线
是抛物线![]() 上一动点,问在抛物线
上一动点,问在抛物线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形?若存在,请直接写出点
为直角顶点的等腰直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() 或4;(2)
或4;(2)![]() ;(3)存在,符合条件的点
;(3)存在,符合条件的点![]() 有4个,
有4个,![]() .
.
【解析】
(1)根据题意得知![]() 与
与![]() 为“郡园牵手抛物线”,即只有一个交点,联立解析式解方程组即可得到答案; (2)由M是第一象限内的点可判断
为“郡园牵手抛物线”,即只有一个交点,联立解析式解方程组即可得到答案; (2)由M是第一象限内的点可判断![]() 的解析式,设出用M的坐标,用M的坐标变量表示出
的解析式,设出用M的坐标,用M的坐标变量表示出![]() ,利用二次函数的性质求最大值即可 ; (3)根据题意画图并求出点B坐标为(-2,2),当抛物线
,利用二次函数的性质求最大值即可 ; (3)根据题意画图并求出点B坐标为(-2,2),当抛物线![]() 分两种情况时依题意构造以C为直角顶点的等腰直角三角形,判断其大致图象,然后根据割补法构造全等三角形,再用待定系数法设出关键点的坐标,并表示出全等三角形边的长度,用对应边相等建立方程组求解即可.
分两种情况时依题意构造以C为直角顶点的等腰直角三角形,判断其大致图象,然后根据割补法构造全等三角形,再用待定系数法设出关键点的坐标,并表示出全等三角形边的长度,用对应边相等建立方程组求解即可.
解:(1)由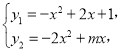 可得:
可得:
![]() ,
,
∵只有一个交点,∴![]() ,
,
∴![]() 或4.
或4.
(2)∵点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的动点,∴
上的动点,∴![]() ,
,
设![]() ,其中
,其中![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() 有最大值,且最大值为
有最大值,且最大值为![]() .
.
(3)存在. 理由如下:
∵B是抛物线![]() 与
与![]() 的“郡园点”.
的“郡园点”.
∴![]() 解得,
解得,![]() ,
,
把![]() 代入
代入![]() 得,
得,![]() ,
,
所以B点坐标为![]() .
.
如图1,
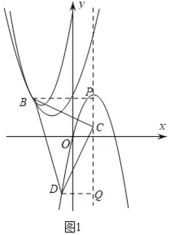
当抛物线![]() 图象为
图象为![]() 时,
时,
过B、D分别作BP、DQ垂直于抛物线对称轴直线![]() ,
,
依题意可设![]() ,且由图可得
,且由图可得![]() .
.
∵△BCD为等腰直角三角形,且C为直角顶点 ,![]()
又∵∠CBP+∠BCP=90° ∴∠BCP+∠DCQ=90°,![]()
在△BCP与△DCQ中,
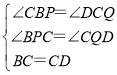
∴△BCP≌△DCQ(AAS) ∴BP=CQ,PC=DQ
即 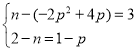
所以由![]() 得
得![]() ,代入得,
,代入得,![]() ,
,
整理得,![]() , 解得,
, 解得,![]() (舍去),
(舍去),
此时C点坐标为![]() .
.
如图2,
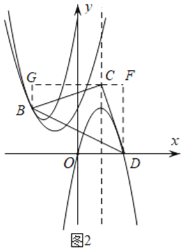
当抛物线![]() 图象为
图象为![]() 时,
时,
过B、D分别作BG、DF分别平行于抛物线的对称轴直线![]() ,且过C作平行于
,且过C作平行于![]() 轴的直线交BG于点G,交DF于点F.
轴的直线交BG于点G,交DF于点F.
依题意可设![]() ,且由图可得
,且由图可得![]() .
.
同理可证△BCG≌△CDF(AAS),所以CG=FD,BG=CF
即 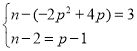 解得,
解得,![]() (舍去),
(舍去),
此时C点坐标为![]() .
.
如图3,
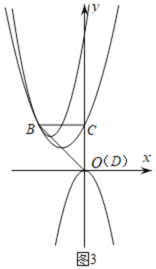
当抛物线![]() 图象为
图象为![]() 时,由△BCD是以C为直角顶点的等腰直角三角形可得BC=CD=2,此时D点与坐标原点O重合,C点坐标为
时,由△BCD是以C为直角顶点的等腰直角三角形可得BC=CD=2,此时D点与坐标原点O重合,C点坐标为![]() .
.
如图4,
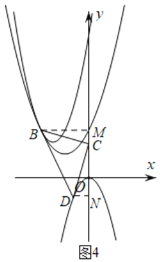
当抛物线![]() 图象为
图象为![]() 时,过B、D分别作BM、DN垂直于y轴交y轴于点M、N.由图可设
时,过B、D分别作BM、DN垂直于y轴交y轴于点M、N.由图可设![]() .
.
同理易证△BCM≌△DCN(AAS) ∴BM=CN,MC=DN
即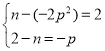 由
由![]() 得
得![]() 并代入得,
并代入得,
![]() 整理得,
整理得,![]() ,
,
解得,![]() ,
,
又∵当![]() 时,过点C且垂直于BC的直线与抛物线
时,过点C且垂直于BC的直线与抛物线![]() 没有交点,故此时D点不存在. ∴此时C点坐标为
没有交点,故此时D点不存在. ∴此时C点坐标为![]() .
.
综上所述,满足题意的C点坐标可以为![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以存在,符合条件的点![]() 有4个,
有4个,![]() ,
,![]() ,
,![]() ,
,![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
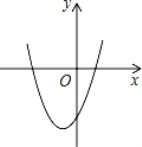
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知![]() ≈1.732,tan20°≈0.36,结果精确到0.1)
≈1.732,tan20°≈0.36,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
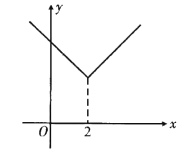
【题目】对于某一函数给出如下定义:对于任意实数![]() ,当自变量
,当自变量![]() 时,函数
时,函数![]() 关于
关于![]() 的函数图象为
的函数图象为![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后得到的函数图象为
翻折后得到的函数图象为![]() ,函数
,函数![]() 的图象由
的图象由![]() 和
和![]() 两部分共同组成,则函数
两部分共同组成,则函数![]() 为原函数的“对折函数”,如函数
为原函数的“对折函数”,如函数![]() (
(![]() )的对折函数为
)的对折函数为![]() .
.
(1)求函数![]() (
(![]() )的对折函数;
)的对折函数;
(2)若点![]() 在函数
在函数![]() (
(![]() )的对折函数的图象上,求
)的对折函数的图象上,求![]() 的值;
的值;
(3)当函数![]() (
(![]() )的对折函数与
)的对折函数与![]() 轴有不同的交点个数时,直接写出
轴有不同的交点个数时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙O的半径为1,点A在x轴的正半轴上,B为⊙O上一点,过点A、B的直线与y轴交于点C,且OA2=ABAC.

(1)求证:直线AB是⊙O的切线;
(2)若AB=![]() ,求直线AB对应的函数表达式.
,求直线AB对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
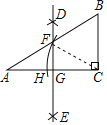
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
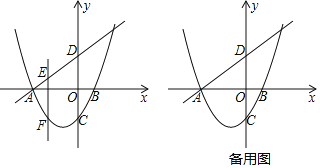
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由;
(3)在平面直角坐标系内存在点G,使得G,E,D,C为顶点的四边形为菱形,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′(点B、C的对应点分别为点B′、C′),连接BB',若AC'∥BB',则∠CAB'的度数为( )

A.45°B.60°C.70°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E为BC边上的一点.连结AE.
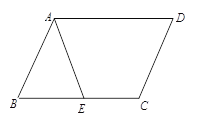
(1)若AB=AE, 求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF︰FA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com