
【题目】如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF.你认为( )

A. 仅小明对 B. 仅小亮对 C. 两人都对 D. 两人都不对
【答案】C
【解析】
分别过点E作EG⊥BC于点G,过点M作MP⊥CD于点P,设EF与MN相交于点O,MP与EF相交于点Q,根据正方形的性质可得EG=MP;对于小明的说法,先利用“HL”证明Rt△EFG≌Rt△MNP,根据全等三角形对应角相等可得∠MNP=∠EFG,再根据角的关系推出∠EQM=∠MNP,然后根据∠MNP+∠NMP=90°得到∠NMP+∠EQM=90°,从而得到∠MOQ=90°,根据垂直的定义即可证得MN⊥EF;对于小亮的说法,先推出∠EQM=∠EFG,∠EQM=∠MNP,然后得到∠EFG=∠MNP,然后利用“角角边”证明△EFG≌△MNP,根据全等三角形对应边相等可得EF=MN.
如图,过点E作EG⊥BC于点G,过点M作MP⊥CD于点P,设EF与MN相交于点O,MP与EF相交于点Q,

∵四边形ABCD是正方形,
∴EG=MP,
对于小明的说法:
在Rt△EFG和Rt△MNP中,
![]() ,
,
∴Rt△EFG≌Rt△MNP(HL),
∴∠MNP=∠EFG,
∵MP⊥CD,∠C=90°,
∴MP∥BC,
∴∠EQM=∠EFG=∠MNP,
又∵∠MNP+∠NMP=90°,
∴∠EQM+∠NMP=90°,
在△MOQ中,∠MOQ=180°-(∠EQM+∠NMP)=180°-90°=90°,
∴MN⊥EF,
故甲正确.
对小亮的说法:
∵MP⊥CD,∠C=90°,
∴MP∥BC,
∴∠EQM=∠EFG,
∵MN⊥EF,
∴∠NMP+∠EQM=90°,
又∵MP⊥CD,
∴∠NMP+∠MNP=90°,
∴∠EQM=∠MNP,
∴∠EFG=∠MNP,
在△EFG和△MNP中,
 ,
,
∴△EFG≌△MNP(AAS),
∴MN=EF,故小亮的说法正确,
综上所述,两个人的说法都正确.
故选C.


科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.7cm
B.10cm
C.12cm
D.22cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.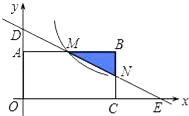
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数 ![]() (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数 ![]() (x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
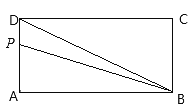
【题目】如图,长方形ABCD中,AB=2cm,BC=4cm,点P按照顺时针方向由点A运动到点D,设点P运动的路程为![]() 图中点P、B、D围成的图形的面积为
图中点P、B、D围成的图形的面积为![]()
(1)写出点P、B、D围成的图形的面积![]() 与
与![]() 之间的关系式和自变量
之间的关系式和自变量![]() 的取值范围;
的取值范围;
(2)当![]() 取何值时,点P、B、D围成的图形的面积等于
取何值时,点P、B、D围成的图形的面积等于![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣1、﹣2、0、1、2、3、4的卡片,除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程 ![]() +
+ ![]() =2的解为正数,且不等式组
=2的解为正数,且不等式组 ![]() 无解的概率是 .
无解的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为![]() .求:(1)求BF+CE的值; (2)求△ABC的周长.
.求:(1)求BF+CE的值; (2)求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中装有大小相同的2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球.
①求第一次摸到绿球,第二次摸到红球的概率;
②求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com