
 如图,Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB的外角平分线CF相交于点D,AD交CB于P,CF交AB的延长线于F,过D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长线交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG,其中正确的有①②③⑤.
如图,Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB的外角平分线CF相交于点D,AD交CB于P,CF交AB的延长线于F,过D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长线交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG,其中正确的有①②③⑤. 分析 (1)设∠GCD=x,∠DAC=y,则:$\left\{\begin{array}{l}{x=y+∠ADC}\\{2x=2y+∠ABC}\end{array}\right.$,故$∠ADC=\frac{1}{2}∠ABC$=45°.
(2)根据三线合一,延长GD与AC相交于点P,则CG=CP,AP=AF;
(3)证△ACD与△AED全等即可,同时可得出三角形CDE是等腰直角三角形;
(4)注意到E是三角形CGF的垂心,从而可证△CHG≌△FHE,则FH=CH=EH+CE=GE+CE=$\sqrt{2}$CD+GH;
(5)在DF上截取DM=CD,证△EMF≌△CEG即可.
解答 解:①利用公式:∠CDA=$\frac{1}{2}$∠ABC=45°,①正确;
②如图:延长GD与AC交于点P',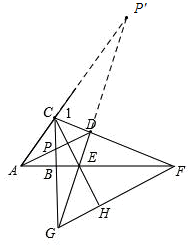
由三线合一可知CG=CP',
∵∠ADC=45°,DG⊥CF,
∴∠EDA=∠CDA=45°,
∴∠ADP=∠ADF,
∴△ADP'≌△ADF(ASA),
∴AF=AP'=AC+CP'=AC+CG,故②正确;
③如图: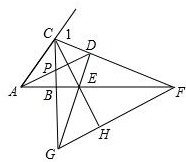
∵∠EDA=∠CDA,
∠CAD=∠EAD,
从而△CAD≌△EAD,
故DC=DE,③正确;
④∵BF⊥CG,GD⊥CF,
∴E为△CGF垂心,
∴CH⊥GF,且△CDE、△CHF、△GHE均为等腰直角三角形,
∴HF=CH=EH+CE=GH+CE=GH+$\sqrt{2}$CD,故④错误;
⑤如图:作ME⊥CE交CF于点M,
则△CEM为等腰直角三角形,从而CD=DM,CM=2CD,EM=EC,
∵∠MFE=∠CGE,
∠CEG=∠EMF=135°,
∴△EMF≌△CEG(AAS),
∴GE=MF,
∴CF=CM+MF=2CD+GE,
故⑤正确;
综上所述,
答案为:①②③⑤.
点评 本题考查了角平分线的性质、等腰三角形的判定与性质、三角形垂心的定义和性质、全等三角形的判定与性质等多个知识点,技巧性很强,难度较大,要求学生具有较高的几何素养.对于这一类多个结论的判断型问题,熟悉常见的结论及重要定理是解决问题的关键,比如对第一个结论的判定,若熟悉该模型则可以秒杀.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
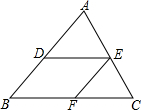 如图,DE∥BC,EF∥AB,则:
如图,DE∥BC,EF∥AB,则:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
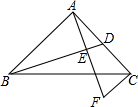 如图,AB⊥AC,AB=AC=$\sqrt{2}$cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=$\frac{\sqrt{2}}{2}$cm.
如图,AB⊥AC,AB=AC=$\sqrt{2}$cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=$\frac{\sqrt{2}}{2}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com