
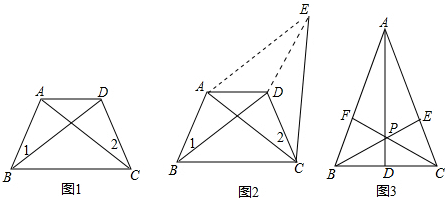
分析 (1)如图2,先证明四边形ABDE是平行四边形,得对角相等,对边相等:∠AED=∠1,AE=BD,AB=ED,根据等量代换得:∠2=∠AED,由AC=AE,得∠ACE=∠AEC,利用等式的性质可知:∠DCE=∠DEC,所以AB=CD;
(2)如图3,作辅助线,构建平行四边形,证明四边形EFGB和BHCE是平行四边形,∠FCB=∠EBC=∠BCH,CH=BE=CF,再证明△BHC≌△BFC,得∠BFC=∠H=∠BEC,根据等式性质得:∠ABE+∠EBC=∠ACF+∠FCB,所以∠ABC=∠ACB,由等角对等边得:AB=AC.
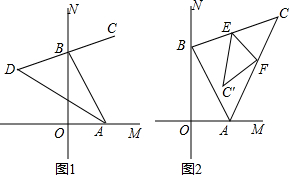
解答 解:(1)如图2,过A作BD的平行线,过D作AB的平行线,二者交于点E,连接CE,
∵AB∥DE,AE∥BD,
∴四边形ABDE是平行四边形,
∴∠AED=∠1,AE=BD,AB=ED,
∵∠1=∠2,
∴∠2=∠AED.
∵AC=BD,AE=BD,
∴AC=AE,
∴∠ACE=∠AEC,
∴∠2+∠DCE=∠AED+∠DEC,
∴∠DCE=∠DEC,
∴DE=DC,
∵AB=DE,
∴AB=CD;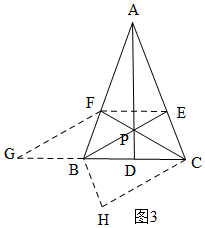
(2)过F作GF,使GF∥BE,且GF=BE,连接EF,
则四边形EFGB是平行四边形,
∴∠G=∠FEB=∠EBC,且GF=BE=FC,
∴∠FCB=∠EBC,
∴∠G=∠FEB=∠EBC=∠FCB,
过C、B分别作CH∥BE,BH∥EC,则四边形BHCE是平行四边形,
∴∠FCB=∠EBC=∠BCH,CH=BE=CF,
∵BC=BC,
∴△BHC≌△BFC,
∴∠BFC=∠H,
∴∠BFC=∠H=∠BEC,
∵∠EPB=∠EPC,
∴∠ABE=∠ACF,
∴∠ABE+∠EBC=∠ACF+∠FCB,
即∠ABC=∠ACB,
∴AB=AC.
点评 本题考查了全等三角形的性质和判定、平行四边形的性质和判定、等腰三角形的性质和判定,本题利用平移的方法解决问题,就是作平行线的方法,构建平行四边形,利用平行四边形的性质:平行四边形的对边相等解决问题,第二问有难度,作辅助线是关键.


科目:初中数学 来源: 题型:选择题
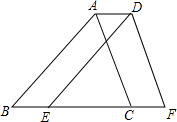 如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )| A. | 2:1 | B. | 3:2 | C. | 4:3 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
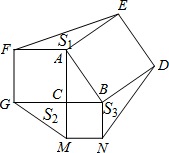 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )| A. | S1=S2=S3 | B. | S1=S2<S3 | C. | S1=S3<S2 | D. | S2=S3<S1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x-1)=21 | B. | x(x+1)=21 | C. | x(x-1)=42 | D. | x(x+1)=42 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
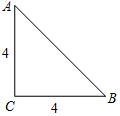 在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.
在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
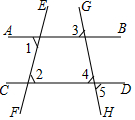 如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.
如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com