
【题目】如图,已知抛物线![]() 与x轴相交于A,B两点,并与直线
与x轴相交于A,B两点,并与直线![]() 交于B,C两点,其中点C是直线
交于B,C两点,其中点C是直线![]() 与y轴的交点,连接AC.
与y轴的交点,连接AC.
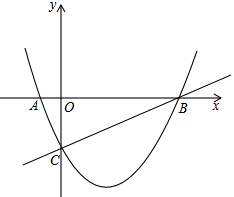
(1)求抛物线的解析式;
(2)证明:△ABC为直角三角形;
(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.
【答案】(1) y=![]() x2-
x2-![]() x-2.(2)证明见解析;(3)
x-2.(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由直线y=![]() x-2交x轴、y轴于B、C两点,则B、C坐标可求.进而代入抛物线y=ax2-
x-2交x轴、y轴于B、C两点,则B、C坐标可求.进而代入抛物线y=ax2-![]() x+c,即得a、c的值,从而有抛物线解析式.
x+c,即得a、c的值,从而有抛物线解析式.
(2)求证三角形为直角三角形,我们通常考虑证明一角为90°或勾股定理.本题中未提及特殊角度,而已知A、B、C坐标,即可知AB、AC、BC,则显然可用勾股定理证明.
(3)在直角三角形中截出矩形,面积最大,我们易得两种情形,①一点为C,AB、AC、BC边上各有一点,②AB边上有两点,AC、BC边上各有一点.讨论时可设矩形一边长x,利用三角形相似等性质表示另一边,进而描述面积函数.利用二次函数最值性质可求得最大面积.
试题解析:(1)∵直线y=![]() x-2交x轴、y轴于B、C两点,
x-2交x轴、y轴于B、C两点,
∴B(4,0),C(0,-2),
∵y=ax2-![]() x+c过B、C两点,
x+c过B、C两点,
∴![]() ,
,
解得 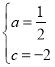 ,
,
∴y=![]() x2-
x2-![]() x-2.
x-2.
(2)如图1,连接AC,
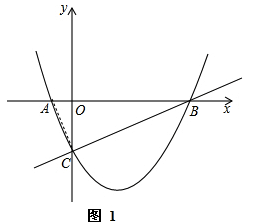
∵y=![]() x2-
x2-![]() x-2与x负半轴交于A点,
x-2与x负半轴交于A点,
∴A(-1,0),
在Rt△AOC中,
∵AO=1,OC=2,
∴AC=![]() ,
,
在Rt△BOC中,
∵BO=4,OC=2,
∴BC=2![]() ,
,
∵AB=AO+BO=1+4=5,
∴AB2=AC2+BC2,
∴△ABC为直角三角形.
(3)△ABC内部可截出面积最大的矩形DEFG,面积为![]() ,理由如下:
,理由如下:
①一点为C,AB、AC、BC边上各有一点,如图2,此时△AGF∽△ACB∽△FEB.
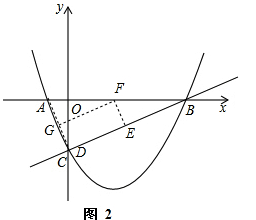
设GC=x,AG=![]() -x,
-x,
∵![]() ,
,
∴![]() ,
,
∴GF=2![]() -2x,
-2x,
∴S=GC![]() GF=x
GF=x![]() (2
(2![]() -2x)=-2x2+2
-2x)=-2x2+2![]() x=-2[(x-
x=-2[(x-![]() )2-
)2-![]() ]=-2(x-
]=-2(x-![]() )2+
)2+![]() ,
,
即当x=![]() 时,S最大,为
时,S最大,为![]() .
.
②AB边上有两点,AC、BC边上各有一点,如图3,此时△CDE∽△CAB∽△GAD,
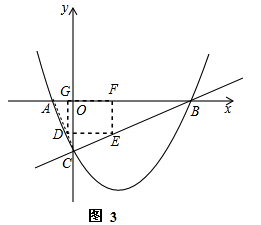
设GD=x,
∵![]() ,
,
∴![]() ,
,
∴AD=![]() x,
x,
∴CD=CA-AD=![]() ,
,
∵![]() ,
,
∴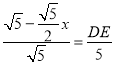 ,
,
∴DE=5-![]() x,
x,
∴S=GD![]() DE=x
DE=x![]() (5-
(5-![]() x)=-
x)=-![]() x2+5x=-
x2+5x=-![]() [(x-1)2-1]=-
[(x-1)2-1]=-![]() (x-1)2+
(x-1)2+![]() .
.
即x=1时,S最大,为![]() .
.
综上所述,△ABC内部可截出面积最大的矩形DEFG,面积为![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.

(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留画图痕迹);
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有红色.白色玻璃球共40个,除颜色外其他完全相同,小明通过多次摸球试验后发现,其中摸到白色球的频率稳定在85%左右,则口袋中红色球可能有( ).
A.34个B.30个C.10个D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆的直径为10cm,如果点P到圆心O的距离是d,则( )
A. 当d=8cm时,点P在⊙O内 B. 当d=10cm时,点P在⊙O上
C. 当d=5cm时,点P在⊙O上 D. 当d=6cm时,点P在⊙O内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com