
【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.

(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)如图,连接OA,由AE为⊙O的切线,BD⊥AE得到∠DAO=∠EDB=90°,于是得到DB∥AO,推出∠DBA=∠BAO,由于OA=OB,得到∠ABC=∠BAO,即可得到结论;
(2)根据三角函数的知识可求出AD,从而根据勾股定理求出AB的长,根据三角函数的知识即可得出⊙O的半径.
试题解析:(1)如图,连接OA,
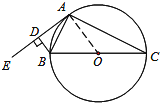
∵AE为⊙O的切线,BD⊥AE,
∴∠DAO=∠EDB=90°,
∴DB∥AO,
∴∠DBA=∠BAO,
又∵OA=OB,
∴∠ABC=∠BAO,
∴∠DBA=∠ABC;
(2)∵BD=1,tan∠BAD=![]() ,
,
∴AD=2,
∴AB=![]() ,
,
∴cos∠DBA=![]() ;
;
∵∠DBA=∠CBA,
∴BC=![]() .
.
∴⊙O的半径为2.5.


科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
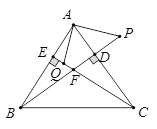
求证:(1)AP=AQ ;
(2)AP⊥AQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上的点E处.
(1)求点E、点D的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F,点P是坐标轴上一点请直接写出使S△CEP=![]() S△COF的点P的坐标.
S△COF的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家环保局统一规定,空气质量分为5级:当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

(1)本次调查共抽取了 天的空气质量检测结果,请补全条形统计图;
(2)扇形统计图中3级空气质量所对应的圆心角为 °;
(3)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,请你估计2015年该城市有多少天不适宜开展户外活动.(说明:2015年共365天)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC纸片沿DE折叠,使点A落在点A′处,且A′B平分∠ABC,A′C平分∠ACB,若∠BA′C=110°,则∠1+∠2=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,∠ABC=45°,BE⊥AC于点E,AD⊥BC于点D,BE与AD相交于F.

(1)求证:BF=AC;
(2)若BF=3,求CE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=3,AD=6,点E是边AD上的一个动点,把△BAE沿BE折叠,若点A的对应点A′恰落在矩形ABCD的对称轴上,则AE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com