
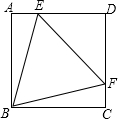
 如图,正方形ABCD中,点E、F分别在AD、DC上,且△BEF为等边三角形.下列结论:①DE=DF;②∠AEB=75°;③AE+CF=EF;④BE=$\sqrt{2}$DE;⑤△EDF与△BFC的面积比为2:1.其中正确的结论有4个.
如图,正方形ABCD中,点E、F分别在AD、DC上,且△BEF为等边三角形.下列结论:①DE=DF;②∠AEB=75°;③AE+CF=EF;④BE=$\sqrt{2}$DE;⑤△EDF与△BFC的面积比为2:1.其中正确的结论有4个. 分析 先证明△ABE≌△CBF,得到AE=CF,∠ABE=∠CBF=15°可以推出①②④正确,设正方形边长为b,DE=DF=a,则EF=BF=$\sqrt{2}$a,在RT△BCF中,利用BF2=BC2+CF2,求出a、b关系即可判定③错误,⑤正确.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠C=∠ABC=∠D=90°,
∵△BEF是等边三角形,
∴BE=BF=EF,∠EBF=60°,
在△ABE和△CBF中,
$\left\{\begin{array}{l}{AB=BC}\\{BE=BF}\end{array}\right.$,
∴△ABE≌△CBF,
∴AE=CF,∠ABE=∠CBF,
∴DE=DF,故①正确,
∠ABE=∠CBF=$\frac{1}{2}$((90°-60°)=15°,
∴∠AEB=90°-∠ABE=75°,故②正确,
∵DE=DF,∠D=90°,
∴∠DEF=∠DFE=45°,
∴EF=$\sqrt{2}$ED,
∴BE=$\sqrt{2}$DE,故④正确.
设正方形边长为b,DE=DF=a,则EF=BF=$\sqrt{2}$a,
在RT△BCF中,
∵BF2=BC2+CF2,
∴2a2=b2+(b-a)2,
∴a2+2ab-2b2=0,
∴a=(-1±$\sqrt{3}$)b,
∵a>O,
∴a=($\sqrt{3}$-1)b,
∴AE=CF=(2-$\sqrt{3}$)b,
∵AE+CF≠b,故③错误.
∵S△DEF:S△BCF=$\frac{1}{2}$[($\sqrt{3}$-1)b]2:$\frac{1}{2}$•b•(2-$\sqrt{3}$)b=2,故⑤正确,
故答案为4.
点评 本题考查正方形的性质、全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,利用参数解决问题,把问题转化为方程解决,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
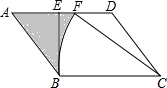 如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为6-$\frac{4}{3}$π.
如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为6-$\frac{4}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=20-2x(0<x<20) | B. | y=20-2x(0<x<10) | C. | y=20-2x(5<x<10) | D. | y=$\frac{20-x}{2}$(5<x<10) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
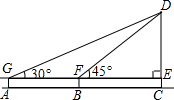 某校数学兴趣小组的同学用学到的解直角三角形的知识,测量聊城摩天轮圆心D到地面AC的高度CD,如图,在空地的A处,他们利用测角仪器测得CD顶端的仰角为30°,沿AC方向前进40米到达B处,又测得CD顶端的仰角为45°,已知测交仪器的高度为1.2米,求摩天轮圆心到地面的高度.($\sqrt{3}$≈1.732,精确到0.1米)
某校数学兴趣小组的同学用学到的解直角三角形的知识,测量聊城摩天轮圆心D到地面AC的高度CD,如图,在空地的A处,他们利用测角仪器测得CD顶端的仰角为30°,沿AC方向前进40米到达B处,又测得CD顶端的仰角为45°,已知测交仪器的高度为1.2米,求摩天轮圆心到地面的高度.($\sqrt{3}$≈1.732,精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{CB}$+$\overrightarrow{BA}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{AC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BC}$-$\overrightarrow{AC}$=$\overrightarrow{0}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{DA}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com