
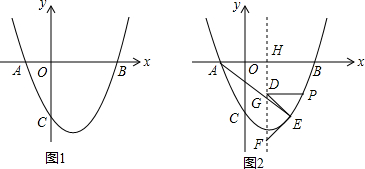
 在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.分析 (1)令y=0,求出x轴交点坐标,再用OB=OC求出C点坐标,代入抛物线方程即可;
(2)先求出直线AC解析式,再用t表示出PN代入面积公式计算即可;
(3)依次求出直线AE的解析式为y=-x-2,直线WG的解析式为y=3x-8,直线KH的解析式为y=-2x+3,直线AV的解析式为y=-$\frac{1}{3}$x-$\frac{2}{3}$,即可.
解答 解:(1)令y=0,则ax2-3ax-10a=0,
即a(x+2)(x-5)=0,
∴x1=-2,x2=5,
∴A(-2,0),B(5,0),
∴OB=5,
∵OB=OC,
∴OC=5,
∴C(0,-5),
∴-5=-10a,
∴a=$\frac{1}{2}$;
(2)如图1,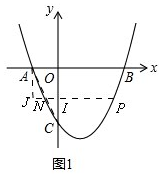
由(1)可知知抛物线解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-5,
设直线AC的解析式为:y=k1x+b,把A、C两点坐标代入得:
$\left\{\begin{array}{l}{0=-2{k}_{1}+b}\\{b=-5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=-\frac{5}{2}}\\{b=-5}\end{array}\right.$,
∴y=-$\frac{5}{2}$x-5,
∵点P的横坐标为t,则P(t,$\frac{1}{2}$t2-$\frac{3}{2}$t-5),
过点P作PN∥x轴交AC于点N,过点A作AJ⊥PN于J,
把y=$\frac{1}{2}$x2-$\frac{3}{2}$x-5,代入直线AC解析式y=-$\frac{5}{2}$x-5中,
解得xN=-$\frac{1}{5}$t2+$\frac{3}{5}$t,
∴N(-$\frac{1}{5}$t2+$\frac{3}{5}$t,$\frac{1}{2}$t2-$\frac{3}{2}$t-5),
∴PN=t-(-$\frac{1}{5}$t2+$\frac{3}{5}$t)=$\frac{1}{5}$t2+$\frac{2}{5}$t,
S=S△ANP+S△CNP=$\frac{1}{2}$PN×AJ+$\frac{1}{2}$PN×AI
=$\frac{1}{2}$PN×OI+$\frac{1}{2}$PN×CI
=$\frac{1}{2}$PN(OI+CI)
=$\frac{1}{2}$PN×OC
=$\frac{1}{2}$t2+t,
(3)由y=$\frac{1}{2}$x2-$\frac{3}{2}$x-5=$\frac{1}{2}$(x-$\frac{3}{2}$)2-$\frac{49}{8}$,
得抛物线的对称轴为直线x=$\frac{3}{2}$,顶点坐标为($\frac{3}{2}$,-$\frac{49}{8}$),
∵$\frac{PD}{FD}=\frac{5}{8}$,
∴设DP=5n,DF=8n,
∵DE=EP=5n,
过点E作EM⊥l于点M,则DM=FM=$\frac{1}{2}$DF=4n,
∴在Rt△DME中,EM=3n,
∴点P的横坐标为5n+$\frac{3}{2}$,点E横坐标为3n+$\frac{3}{2}$,
∴yP=$\frac{1}{2}$(5n+$\frac{3}{2}$-$\frac{3}{2}$)2-$\frac{49}{8}$=$\frac{25}{2}$n2-$\frac{49}{8}$,
yE=$\frac{1}{2}$(3n+$\frac{3}{2}$-$\frac{3}{2}$)2-$\frac{49}{8}$=$\frac{9}{2}$n2-$\frac{49}{8}$
∴D($\frac{3}{2}$,$\frac{25}{2}$n2-$\frac{49}{8}$),M($\frac{3}{2}$,$\frac{9}{2}$n2-$\frac{49}{8}$),
∴DM=$\frac{25}{2}$n2-$\frac{49}{8}$-($\frac{9}{2}$n2-$\frac{49}{8}$)=8n2,
∴8n2=4n,
∴n=$\frac{1}{2}$,
∴E(3,-5),
∵A(-2,0),E(3,-5),
∴直线AE的解析式为y=-x-2,
令x=$\frac{3}{2}$,则y=-x-2=-$\frac{3}{2}$-2=-$\frac{7}{2}$,
∴G($\frac{3}{2}$,-$\frac{7}{2}$),
∵直线y=kx-$\frac{8}{3}$k(k≠0)恰好经过点G,
∴-$\frac{7}{2}$=$\frac{3}{2}$k-$\frac{8}{3}$k,
∴k=3,
∴直线WG的解析式为y=3x-8,
如图2,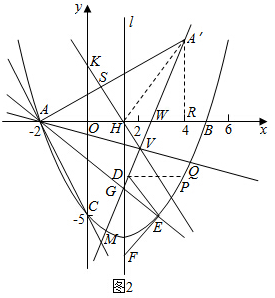
点A关于HK的对称点A′(m,3m-8),
∵A(-2,0),H($\frac{3}{2}$,0),
∴AH=$\frac{7}{2}$,
∵HS垂直平分AA′,
∴A′H=AH=$\frac{7}{2}$,
过A′作A′R⊥x轴于R,
在Rt△A′HR中,A′R2+HR2=A′H2,
∴(3m-8)2+(m-$\frac{3}{2}$)2=$\frac{49}{4}$,
∴m1=$\frac{3}{2}$(舍),m2=$\frac{18}{5}$,
∴A′($\frac{18}{5}$,$\frac{14}{5}$),
∴tan∠A′AR=$\frac{A′R}{AR}$=$\frac{1}{2}$,
∵∠HAS+∠AHS=∠OKH+∠AHS=90°,
∴tan∠OKH=tan∠A′AR=$\frac{1}{2}$,
∴tan∠OKH=$\frac{OH}{OK}$=$\frac{1}{2}$,
∴OK=3,
∴K(0,3),
∴直线KH的解析式为y=-2x+3,
∵$\left\{\begin{array}{l}{y=-2x+3}\\{y=3x-8}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{11}{5}}\\{y=-\frac{7}{5}}\end{array}\right.$,
∴V($\frac{11}{5}$,-$\frac{7}{5}$),
∵A(-2,0),
∴直线AV的解析式为y=-$\frac{1}{3}$x-$\frac{2}{3}$,
设Q(s,$\frac{1}{2}$s2-$\frac{3}{2}$s-5),代入y=-$\frac{1}{3}$x-$\frac{2}{3}$中,
$\frac{1}{2}$s2-$\frac{3}{2}$s-5=-$\frac{1}{3}$s-$\frac{2}{3}$,
∴s1=-2(舍),s2=$\frac{13}{3}$,
∴Q($\frac{13}{3}$,-$\frac{19}{9}$).
点评 此题是二次函数综合题,主要考查了待定系数法求函数解析式,图形面积的计算,解本题的关键是确定确定出直线解析式.


科目:初中数学 来源:2017届重庆市九年级3月月考数学试卷(解析版) 题型:单选题
已知关于 的方程x2-kx-6=0的一个要根为x=3,则实数k的值为( )
的方程x2-kx-6=0的一个要根为x=3,则实数k的值为( )
A. 1 B. - 1 C. 2 D. -2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,AB=5cm,BC=8cm,∠B=60°,G是CD的中点,E是边AD上的动点EG的延长线与BC的延长线交于点F,连结CE,DF.
如图,在平行四边形ABCD中,AB=5cm,BC=8cm,∠B=60°,G是CD的中点,E是边AD上的动点EG的延长线与BC的延长线交于点F,连结CE,DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
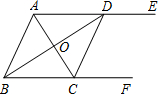 如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
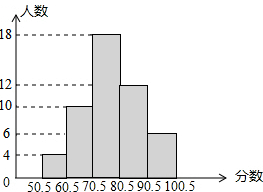 某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述不正确的是( )
某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述不正确的是( )| A. | 抽样的学生共50人 | |
| B. | 50.5-60.5这一分数段的频率为0.08 | |
| C. | 估计优秀率(80分以上为优秀)在36%左右 | |
| D. | 60.5-70.5这一分数段的频数为12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
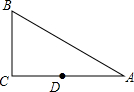 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着直线BD翻折后,点A将在点E处,如果AD⊥DE,那么DE的长度为$4\sqrt{3}$-4.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着直线BD翻折后,点A将在点E处,如果AD⊥DE,那么DE的长度为$4\sqrt{3}$-4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com