
【题目】(2019·信阳一模)如图,锐角三角形ABC中,BC=6,BC边上的高为4,直线MN交边AB于点M,交AC于点N,且MN∥BC,以MN为边作正方形MNPQ,设其边长为x(x>0),正方形MNPQ与△ABC公共部分的面积为y,则y与x的函数图象大致是( )

A.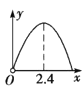 B.
B. C.
C.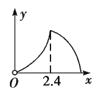 D.
D.
科目:初中数学 来源: 题型:
【题目】为了了解初一年级学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
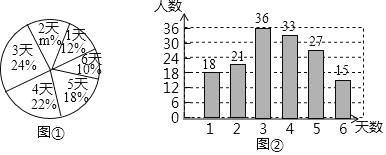
(I)本次随机抽样调查的学生人数为 ,图①中的m的值为 ;
(II)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(III)若该区初一年级共有学生2500人,请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)如图1,![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 到直线
到直线![]() 的距离为2,点
的距离为2,点![]() 到
到![]() 的距离为1,
的距离为1,![]() ,
,![]() ,则
,则![]() 的最小值是______;(提示:将线段
的最小值是______;(提示:将线段![]() 沿
沿![]() 方向平移1个单位长度即可解决,如图2所示.)
方向平移1个单位长度即可解决,如图2所示.)
(关联运用)如图3,在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() 在直线
在直线![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 的最小值是______.
的最小值是______.
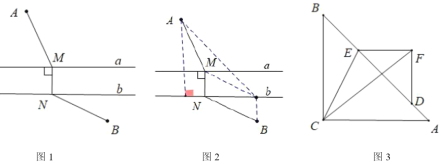
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
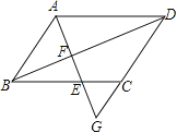
【题目】如图,在平行四边形ABCD中,点G在边DC的延长线上,AG交边BC于点E,交对角线BD于点F.
(1)求证:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费120元,购进A品牌文具袋3个和B品牌文具袋4个共花费88元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为w元.
①求w关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不低于进货价格的45%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交与O点,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列4个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④CF=BD.正确的结论是( )
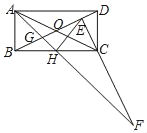
A.①②④B.①④C.③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②![]() >0;③ac﹣b+1=0;④2a+b=0其中正确结论的个数是( )
>0;③ac﹣b+1=0;④2a+b=0其中正确结论的个数是( )
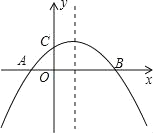
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com