
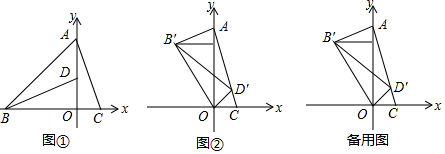
分析 (Ⅰ)延长BD交AC于M,由SAS证明△AOC≌△BOD,得出对应角相等,即可得出结论;
(Ⅱ)作OF⊥AC于F,OE⊥AB′于E,由旋转的性质得出∠BOD=∠B′OD′=90°,OB=OB′,由矩形的性质得出OF=AE,求出点B(-3,0),得出OB=OA=OB′,证出AE=EB′,由勾股定理得出AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,由三角形的面积求出OF=$\frac{3\sqrt{10}}{10}$,得出AB'=2AE=2OF=$\frac{3\sqrt{10}}{5}$即可;
(Ⅲ)由待定系数法求出直线AC的解析式为y=-3x+3,得出直线OE的解析式为y=-3x,直线AB'的解析式为y=$\frac{1}{3}$x+3,解方程组$\left\{\begin{array}{l}{y=-3x}\\{y=\frac{1}{3}x+3}\end{array}\right.$得出点E的坐标,设B'(a,b),由中点坐标公式即可得出答案.
解答 (Ⅰ)证明: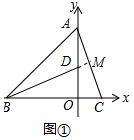 延长BD交AC于M,如图①所示:
延长BD交AC于M,如图①所示:
∵点A(0,3),点B(-3,0),点C(1,0),点D(0,1),
∴OA=OB=3,OC=OD=1,
在△AOC和△BOD中,$\left\{\begin{array}{l}{OA=OB}&{\;}\\{∠AOC=∠BOD}&{\;}\\{OC=OD}&{\;}\end{array}\right.$,
∴△AOC≌△BOD(SAS),
∴∠OAC=∠OBD,
∵∠OAC+∠ACO=90°,
∴∠OBD+∠ACO=90°,
∴∠BMC=90°,
∴BD⊥AC;
(Ⅱ)解:作OF⊥AC于F,OE⊥AB′于E,如图②所示: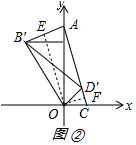
∵将△BOD绕着点O旋转,得到△B′OD′,∠BOD=90°,
∴∠B′OD′=90°,OB=OB′,
∴四边形OFAE是矩形,
∴OF=AE,
∵点A(0,3),点B(-3,0),
∴OB=OA=OB′,
∵OE⊥AB′,
∴AE=EB′,
由勾股定理得:AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
由三角形的面积得:AC•OF=OA•OC,
∴OF=$\frac{OA•OC}{AC}$=$\frac{3×1}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$,
∴AB'=2AE=2OF=$\frac{3\sqrt{10}}{5}$;
(Ⅲ)解:设直线AC的解析式为y=kx+b,
根据题意得:$\left\{\begin{array}{l}{k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=3}\end{array}\right.$,
∴直线AC的解析式为y=-3x+3,
∵OE∥AC,AB'⊥AC,
∴直线OE的解析式为y=-3x,直线AB'的解析式为y=$\frac{1}{3}$x+3,
解方程组$\left\{\begin{array}{l}{y=-3x}\\{y=\frac{1}{3}x+3}\end{array}\right.$得:$\left\{\begin{array}{l}{x=-\frac{9}{10}}\\{y=\frac{27}{10}}\end{array}\right.$,
即E(-$\frac{9}{10}$,$\frac{27}{10}$),
设B'(a,b),由中点坐标公式得:$\frac{a+0}{2}$=-$\frac{9}{10}$,$\frac{b+3}{2}=\frac{27}{10}$,
解得:a=-$\frac{9}{5}$,b=$\frac{12}{5}$,
∴B'(-$\frac{9}{5}$,$\frac{12}{5}$).
点评 本题是三角形综合题目,考查了全等三角形的判定与性质、勾股定理、三角形面积的计算方法、一次函数解析式的求法、两条直线的位置关系等知识;本题综合性强,有一定难度.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:解答题
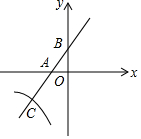 如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.
如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
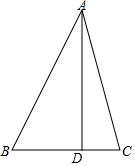 已知△ABC中,AD⊥BC于点D,∠BAC=45°,BD=6,CD=4,
已知△ABC中,AD⊥BC于点D,∠BAC=45°,BD=6,CD=4,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
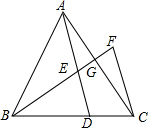 如图,已知△ABC中,D、G分别是边BC、AC上的点,连AD、BC相交于点E,BE=BD.过点C作AD的平行线与BG的延长线于点F,$\frac{CD}{BD}$=$\frac{1}{2}$,$\frac{DE}{EA}$=$\frac{2}{3}$.
如图,已知△ABC中,D、G分别是边BC、AC上的点,连AD、BC相交于点E,BE=BD.过点C作AD的平行线与BG的延长线于点F,$\frac{CD}{BD}$=$\frac{1}{2}$,$\frac{DE}{EA}$=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
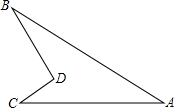 如图为一机器零件,∠A=36°的时候是合格的,小明测得∠BDC=98°,∠C=38°,∠B=23°.
如图为一机器零件,∠A=36°的时候是合格的,小明测得∠BDC=98°,∠C=38°,∠B=23°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com