
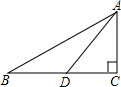
 解:如图,∵BC=12cm,AD是BC边上的中线,
解:如图,∵BC=12cm,AD是BC边上的中线,| 1 |
| 2 |
| AD2-CD2 |
| 102-62 |
| AC2+BC2 |
| 82+122 |
| 13 |
| AC |
| AB |
| 8 | ||
4
|
2
| ||
| 13 |
2
| ||
| 13 |


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 5 |
| 14 |
| 4 |
| 25 |
| 1 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
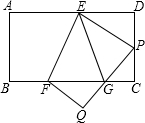 已知矩形纸片ABCD中,AD=6,CD=4,将纸片折叠,使点A落在CD边上点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
已知矩形纸片ABCD中,AD=6,CD=4,将纸片折叠,使点A落在CD边上点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
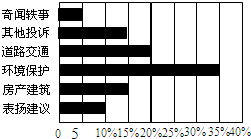 如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共7 0个,请回答下列问题:
如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共7 0个,请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com