
分析 可求得抛物线的对称轴为x=a,再分a<-2、-2≤a≤1和a>1三种情况,根据二次函数的单调性分别求得函数的最小值,即可得到a与n的关系式.
解答 解:
∵y=x2-2ax+1=(x-a)2+1-a2,
∴函数的对称轴方程为x=a,开口向上,
当a<-2时,在-2≤x≤1上,y随x的增大而增大,
∴当x=-2时,y有最小值,最小值为5+4a,即n=5+4a;
当-2≤a≤1时,在-2≤x≤1上,y有最小值1-a2,即n=1-a2;
当a>1时,在-2≤x≤1上,y随x的增大而减小,
∴当x=1时,y有最小值,最小值为2-2a,即n=2-2a;
综上可知n=$\left\{\begin{array}{l}{5+4a(a<-2)}\\{1-{a}^{2}(-2≤a≤1)}\\{2-2a(a>1)}\end{array}\right.$.
点评 本题主要考查二次函数的最值,掌握二次函数的单调性是解题的关键,注意分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<3 | B. | m≤3 | C. | m>3 | D. | m≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
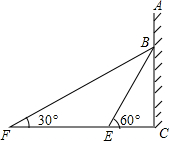 如图,在某建筑物AC上挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行40米到达点E处,看到条幅顶端B,测得仰角为60°.
如图,在某建筑物AC上挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行40米到达点E处,看到条幅顶端B,测得仰角为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com