
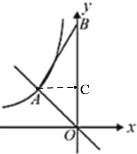
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象交于
的图象交于![]() 点,点
点,点![]() 为
为![]() 轴正半轴上一点,且
轴正半轴上一点,且![]() ,
,![]() 的面积是
的面积是![]() ,则
,则![]() _______.
_______.

【答案】-2
【解析】
如图,过A作AC⊥y轴于C,由一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象交于
的图象交于![]() 点可设A(a,-a),可得k=-a2,由a<0,可得AC=-a,OC=-a,利用∠ABO的正切值可用a表示出BC的长,进而可表示出OB的长,根据△AOB的面积列方程可求出a值,进而可求出k的值.
点可设A(a,-a),可得k=-a2,由a<0,可得AC=-a,OC=-a,利用∠ABO的正切值可用a表示出BC的长,进而可表示出OB的长,根据△AOB的面积列方程可求出a值,进而可求出k的值.
如图,过A作AC⊥y轴于C,
∵一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象交于
的图象交于![]() 点,
点,
∴设A(a,-a),则k=-a2,
∵a<0,
∴AC=-a,OC=-a,
∵∠ABO=30°,
∴BC=![]() =-
=-![]() a,
a,
∴OB=OC+BC=-a-![]() a,
a,
∵△AOB的面积是![]() ,
,
∴![]() OB·AC=
OB·AC=![]() (-a-
(-a-![]() a)(-a)=
a)(-a)=![]() ,
,
解得:a=-![]() ,(正值舍去)
,(正值舍去)
∴k=-a2=-2,
故答案为:-2


科目:初中数学 来源: 题型:
【题目】星星和阳阳是一对双胞胎,他们的爸爸买了两件不同图案的T恤给他们,星星和阳阳都想先挑选.于是阳阳设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的![]() 个小球,上面分别标有数字
个小球,上面分别标有数字![]() .一人先从袋中随机摸出一个小球,另一人再从袋中剩下的
.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的![]() 个小球中随机摸出一个小球.若摸出的两个小球上的数字之和为偶数,则星星先挑选;否则阳阳先挑选.
个小球中随机摸出一个小球.若摸出的两个小球上的数字之和为偶数,则星星先挑选;否则阳阳先挑选.
(1)用树状图或列表法求出星星先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
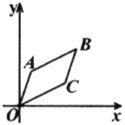
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() ,若将
,若将![]() 先沿
先沿![]() 轴进行第一次对称变换,所得图形沿
轴进行第一次对称变换,所得图形沿![]() 轴进行第二次对称变换,轴对称变换的对称轴遵循
轴进行第二次对称变换,轴对称变换的对称轴遵循![]() 轴、
轴、![]() 轴、
轴、![]() 轴、
轴、![]() 轴…的规律进行,则经过第2018次变换后,
轴…的规律进行,则经过第2018次变换后,![]() 顶点
顶点![]() 坐标为()
坐标为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
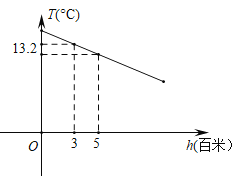
【题目】某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2经过点A(4,0)、B(1,0)两点,点C为抛物线与y轴的交点.
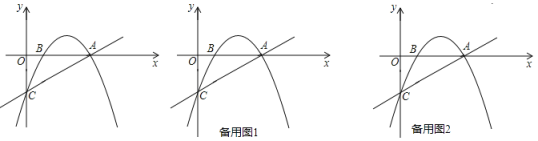
(1)求此抛物线的解析式;
(2)P是x轴上方抛物线上的一个动点,过P作PM⊥x轴,垂足为M,问:是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线上找一点D,过点D作x轴的垂线,交AC于点E,是否存在这样的点D,使DE最长,若存在,求出点D的坐标,以及此时DE的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点A(
过点A(![]() ,2),且与直线
,2),且与直线![]() 交于B、C两点,点B的坐标为(
交于B、C两点,点B的坐标为(![]() ,m).
,m).
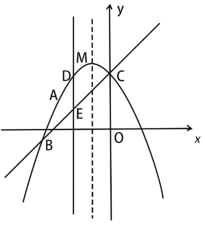
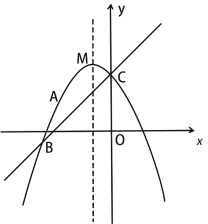
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线BC上方的一点,过点D作DE⊥x轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求PD+PA的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使得∠AQM=45°?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
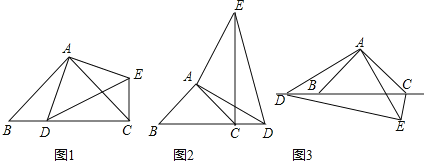
【题目】已知![]() 中,
中,![]() ,
,![]() ,点D为直线BC上的一动点
,点D为直线BC上的一动点![]() 点D不与点B、C重合
点D不与点B、C重合![]() ,以AD为边作
,以AD为边作![]() ,使
,使![]() ,
,![]() ,连接CE.
,连接CE.
发现问题:
如图1,当点D在边BC上时,
![]() 请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
请写出BD和CE之间的位置关系为______,并猜想BC和CE、CD之间的数量关系:______.
尝试探究:
![]() 如图2,当点D在边BC的延长线上且其他条件不变时,
如图2,当点D在边BC的延长线上且其他条件不变时,![]() 中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
拓展延伸:
![]() 如图3,当点D在边CB的延长线上且其他条件不变时,若
如图3,当点D在边CB的延长线上且其他条件不变时,若![]() ,
,![]() ,求线段ED的长.
,求线段ED的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com