
【题目】“2017年张学友演唱会”于6月3日在我市观山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
【答案】
(1)解:设小张跑步的平均速度为x米/分钟,则小张骑车的平均速度为1.5x米/分钟,
根据题意得: ![]() ﹣
﹣ ![]() =4,
=4,
解得:x=210,
经检验,x=210是原方程组的解.
答:小张跑步的平均速度为210米/分钟.
(2)解:小张跑步到家所需时间为2520÷210=12(分钟),
小张骑车所用时间为12﹣4=8(分钟),
小张从开始跑步回家到赶回奥体中心所需时间为12+8+5=25(分钟),
∵25>23,
∴小张不能在演唱会开始前赶到奥体中心.
【解析】(1)由已知条件设小张跑步的平均速度为x米/分钟,则小张骑车的平均速度为1.5x米/分钟,根据等量关系列出关于x的分式方程,解之并检验后即可得出所求答案;
(2)先根据已知条件计算出出小张赶回奥体中心所需时间,将其与23进行比较后即可得出他能否在演唱会开始前赶到奥体中心.
【考点精析】解答此题的关键在于理解分式方程的应用的相关知识,掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
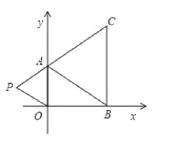
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a.b.c满足关系式![]() ,c是64的算术平方根.
,c是64的算术平方根.
(1)直接写出a,b,c的值:a=____,b=____,c= ____;
(2)如果在第二象限内有一点P(m,2),请用含m的式子表示四边形APOB的面积S![]() ;
;
(3)在(2)的条件下,是否存在点P,使四边形APOB的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
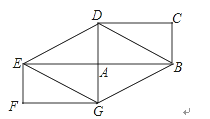
【题目】如图,矩形ABCD和矩形AEFG关于点A中心对称,
(1)四边形BDEG是菱形吗?请说明理由.
(2)若矩形ABCD面积为8,求四边形BDEG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
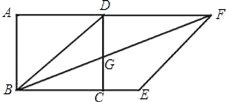
【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 . 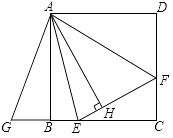
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com