
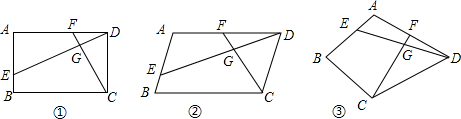
 已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.分析 (1)由矩形的性质得出∠A=∠ADC=90°,由角的互余关系整除∠ADE=∠DCF,即可得出△ADE∽△DCF;
(2)在AD的延长线上取点M,使CM=CF,由等腰三角形的性质得出∠CMF=∠CFM.由平行四边形的性质得出∠A=∠CDM,∠FCB=∠CFM,证出∠BEG+∠FCB=180°,得出∠AED=∠FCB,因此∠CMF=∠AED.证明△ADE∽△DCM,得出对应边成比例$\frac{DE}{CM}=\frac{AD}{CD}$,即可得出结论;
(3)连接AC、BD,交于点M,作CN⊥AD于N,由勾股定理求出BD,由SSS证明△ABD≌△CBD,得出∠ABD=∠CBD,由等腰三角形的性质得出AM=CM,∠AMD=90°=∠BAD,证明△ABD∽△MAD,得出对应边成比例求出DM,由勾股定理求出AM,由△ACD的面积求出CN,证明△ADE∽△NCF,得出对应边成比例,即可得出结果.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠ADE+∠CDG=90°,
又∵DE⊥CF,∠CDG+∠DCF=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF.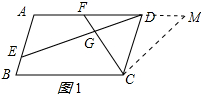
(2)解:当∠B+∠EGC=180°时,$\frac{DE}{CF}=\frac{AD}{CD}$成立,理由如下:
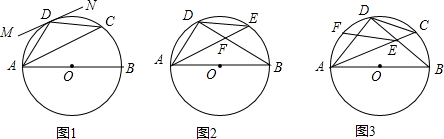
在AD的延长线上取点M,使CM=CF,如图1所示:
则∠CMF=∠CFM.∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A=∠CDM,∠FCB=∠CFM,
∵∠B+∠EGC=180°,
∴∠BEG+∠FCB=360°-(∠B+∠EGC)=180°,
又∵∠BEG+∠AED=180°,
∴∠AED=∠FCB,
∴∠CMF=∠AED.
∴△ADE∽△DCM,
∴$\frac{DE}{CM}=\frac{AD}{CD}$,
∴$\frac{DE}{CF}=\frac{AD}{CD}$;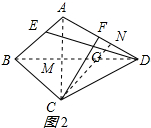
(3)解:$\frac{DE}{CF}=\frac{25}{24}$;理由如下:
连接AC、BD,交于点M,作CN⊥AD于N,如图2所示:
∵∠BAD=90°,AB=6,AD=8,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
在△ABD和△CBD中,$\left\{\begin{array}{l}{AB=CB}\\{DA=DC}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD,
∵AB=CB,
∴BD⊥AC,AM=CM,
∴∠AMD=90°=∠BAD,
又∵∠ADB=∠MDA,
∴△ABD∽△MAD,
∴AD:DM=BD:AD,
∴AD2=BD•DM,即82=10DM,
∴DM=6.4,
∴AM=$\sqrt{A{D}^{2}-D{M}^{2}}$=$\sqrt{{8}^{2}-6.{4}^{2}}$=4.8,
∴AC=2AM=9.6,
∵△ACD的面积=$\frac{1}{2}$AD•CN=$\frac{1}{2}$AC•DM,
∴8×CN=9.6×6.4,
解得:CN=7.68,
∵DE⊥CF,
∴∠CFN=∠DAE,
∵CN⊥AD,
∴∠CNF=90°=∠DAE,
∴△ADE∽△NCF,
∴$\frac{DE}{CF}=\frac{AD}{CN}$=$\frac{8}{7.68}$=$\frac{25}{24}$.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、勾股定理、三角形面积的计算等知识;熟练掌握等腰三角形的性质,证明三角形全等和三角形相似是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
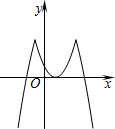 如图,将抛物线y=(x-1)2 的图象位于直线y=4以上的部分向下翻折,得到新的图象(实线部分),若直线y=-x+m与新图象只有四个交点,求m的取值范围.( )
如图,将抛物线y=(x-1)2 的图象位于直线y=4以上的部分向下翻折,得到新的图象(实线部分),若直线y=-x+m与新图象只有四个交点,求m的取值范围.( )| A. | $\frac{3}{4}$<m<3 | B. | $\frac{3}{4}$<m<7 | C. | $\frac{4}{3}$<m<7 | D. | $\frac{4}{3}$<m<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
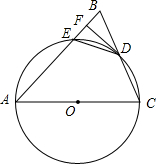 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2+a}{{-4-4a-{a^2}}}$ | B. | $\frac{a-b}{b-a}$ | C. | $\frac{{{x^2}-4}}{x-2}$ | D. | $\frac{{{x^2}+{y^2}}}{x+y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
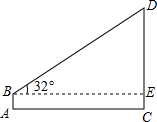 在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com