
分析 (1)首先利用二次根式乘除运算法则化简二次根式进而求出答案;
(2)首先利用绝对值以及二次根式乘法运算法则求出答案.
解答 解:(1)$\sqrt{81}$+$\sqrt{(-3)^{2}}$×$\sqrt{\frac{16}{9}}$-$\sqrt{12\frac{1}{4}}$÷$\root{3}{-27}$
=9+4-$\frac{7}{2}$×(-$\frac{1}{3}$)
=13+$\frac{7}{6}$
=14$\frac{1}{6}$;
(2)3$\sqrt{2}$+|$\sqrt{2}$-3|-(-3$\sqrt{2}$)2-$\sqrt{2}$($\sqrt{2}$-1)
=3$\sqrt{2}$+3-$\sqrt{2}$-18-2+$\sqrt{2}$
=3$\sqrt{2}$-17.
点评 此题主要考查了二次根式的混合运算以及绝对值的性质,正确化简二次根式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在锐角三角形ABC中,BC=5$\sqrt{2}$,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是5.
在锐角三角形ABC中,BC=5$\sqrt{2}$,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
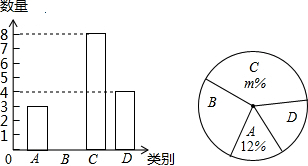
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.
如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
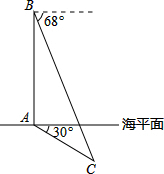 在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方325米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{3}$≈1.7)
在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方325米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com