
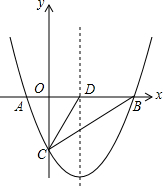
 ��ͼ��������y=$\frac{1}{2}$x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0����C��0��-2����
��ͼ��������y=$\frac{1}{2}$x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0����C��0��-2�������� ��1���ɴ���ϵ����������Ԫһ�η��������m��n��ֵ���ɣ�
��2����ͼ1�У��������������ۢٵ�PD=DCʱ����CP=CDʱ���ֱ�д����P���꼴�ɣ�
��3�������BC�Ľ���ʽ�������E�ĺ�����Ϊa�����ı���CDBF�����=S��BCD+S��CEF+S��BEF���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
��� �⣺��1����A��-1��0����C��0��-2����������y=$\frac{1}{2}$x2+mx+n�ϣ�
��$\left\{\begin{array}{l}{n=-2}\\{\frac{1}{2}-m+n=0}\end{array}\right.$
��$\left\{\begin{array}{l}{m=-\frac{3}{2}}\\{n=-2}\end{array}\right.$��
�������߽���ʽΪy=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
��2�����ڣ�
���ɣ���C��0��-2����D��$\frac{3}{2}$��0����
��CD=$\sqrt{{2}^{2}+��\frac{3}{2}��^{2}}$=$\frac{5}{2}$��
�ٵ�PD=DCʱ����P���꣨$\frac{3}{2}$��$\frac{5}{2}$����$\frac{3}{2}$��-$\frac{5}{2}$����
�ڵ�CP=CDʱ����P���꣨$\frac{3}{2}$��-4����
�൱��P���꣨$\frac{3}{2}$��$\frac{5}{2}$����$\frac{3}{2}$��-$\frac{5}{2}$����$\frac{3}{2}$��-4��ʱ����PCD����CDΪ���ĵ��������Σ�
��3����y=0����$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0�����x=4��-1��
���B���꣨4��0����
��ֱ��BCΪy=kx+b����$\left\{\begin{array}{l}{4k+b=0}\\{b=-2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$��
��ֱ��BC����ʽΪy=$\frac{1}{2}$x-2��
�����E�ĺ�����Ϊa��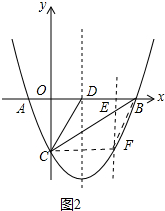
��EF=Ey-Fy=-$\frac{1}{2}$a2+2a��0��a��4����
��S�ı���CDBF=S��BCD+S��CEF+S��BEF
=$\frac{1}{2}$BD��OC+$\frac{1}{2}$EF��CM+$\frac{1}{2}$EF��BN
=$\frac{1}{2}$��$\frac{5}{2}$��2+$\frac{1}{2}$����-$\frac{1}{2}$a2+2a����4
=-a2+4a+$\frac{5}{2}$
=-��a-2��2+$\frac{13}{2}$����
��a=2ʱ���ı���CDBF������ʱ��E���꣨2��-1����
���ʱ��E��BC�е㣬
�൱��E�˶���BC�е�ʱ���ı���CDBF������������Ϊ$\frac{13}{2}$����ʱ��E���꣨2��-1����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ������һ�κ����Ľ���ʽ�����ã����κ����Ľ���ʽ�����ã����ɶ��������ã����������ε����ʵ����ã��ı��ε���������ã����ʱ��������Ľ���ʽ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
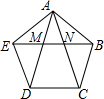 ��ͼ�����������ABCDE�У��Խ���AD��AC��EB�ֱ��ڵ�M��N�������н�����ȷ���ǣ�������
��ͼ�����������ABCDE�У��Խ���AD��AC��EB�ֱ��ڵ�M��N�������н�����ȷ���ǣ�������| A�� | EM��AE=2��$��\sqrt{5}-1��$ | B�� | MN��EM=$��\sqrt{5}-1��$��$��3-\sqrt{5}��$ | C�� | AM��MN=$��3-\sqrt{5}��$��$��\sqrt{5}-1��$ | D�� | MN��DC=$��3-\sqrt{5}��$��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����ѧ�ڵ���ѧ�ɼ������ʾ����λ���֣�
С����ѧ�ڵ���ѧ�ɼ������ʾ����λ���֣�| ������� | ƽʱ | ���п��� | ��ĩ���� | |||
| ����1 | ����2 | ����3 | ����4 | |||
| �ɼ� | 107 | 110 | 114 | 109 | 110 | 115 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
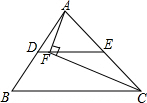 ��ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC���е㣬AC=12��F��DE��һ�㣬��DF=1������AF��CF������AFC=90�㣬��BC�ij���Ϊ��������
��ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC���е㣬AC=12��F��DE��һ�㣬��DF=1������AF��CF������AFC=90�㣬��BC�ij���Ϊ��������| A�� | 12 | B�� | 13 | C�� | 14 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3-x����3+x��=9-x2 | B�� | ��y+1����y-3��=��3-y����y+1�� | ||
| C�� | 4yz-2y2z+z=2y��2z-zy��+z | D�� | -8x2+8x-2=-2��2x-1��2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com