
【题目】已知如图,在数轴上点![]() ,
, ![]() 所对应的数是
所对应的数是![]() ,
, ![]() .
.
对于关于![]() 的代数式
的代数式![]() ,我们规定:当有理数
,我们规定:当有理数![]() 在数轴上所对应的点为
在数轴上所对应的点为![]() 之间(包括点
之间(包括点![]() ,
, ![]() )的任意一点时,代数式
)的任意一点时,代数式![]() 取得所有值的最大值小于等于
取得所有值的最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,则称代数式
,则称代数式![]() ,是线段
,是线段![]() 的封闭代数式.
的封闭代数式.
例如,对于关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,代数式
时,代数式![]() 取得最大值是
取得最大值是![]() ;当
;当![]() 时,代数式
时,代数式![]() 取得最小值是
取得最小值是![]() ,所以代数式
,所以代数式![]() 是线段
是线段![]() 的封闭代数式.
的封闭代数式.
问题:(![]() )关于
)关于![]() 代数式
代数式![]() ,当有理数
,当有理数![]() 在数轴上所对应的点为
在数轴上所对应的点为![]() 之间(包括点
之间(包括点![]() ,
, ![]() )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.
所以代数式![]() __________(填是或不是)线段
__________(填是或不是)线段![]() 的封闭代数式.
的封闭代数式.
(![]() )以下关
)以下关![]() 的代数式:
的代数式:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
是线段![]() 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段![]() 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).
(![]() )关于
)关于![]() 的代数式
的代数式![]() 是线段
是线段![]() 的封闭代数式,则有理数
的封闭代数式,则有理数![]() 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.
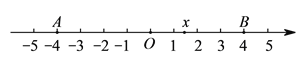
【答案】(![]() )见解析(
)见解析(![]() )④(
)④(![]() )
)![]() ;
; ![]()
【解析】试题分析:(1)观察数轴,当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,当
,当![]() 时,
时, ![]() 取得最小值为
取得最小值为![]() ,所以代数式
,所以代数式![]() 不是线段
不是线段![]() 的封闭代数式;
的封闭代数式;
(2)按照封闭代数式的定义,逐个分析即可;
(3)观察代数式可知,当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,列方程求出x的值;当
,列方程求出x的值;当![]() 时,
时,
![]() 取得最小值为
取得最小值为![]() ,列方程求出x的值;然后从中选出最大的和最小的.
,列方程求出x的值;然后从中选出最大的和最小的.
(![]() )解:当
)解:当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,
,
当![]() 时,
时, ![]() 取得最小值为
取得最小值为![]() ,
,
∵![]() 的最大值
的最大值![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
(![]() )证明:①∵
)证明:①∵ ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 的最小值为
的最小值为![]() ,不满足最小值大于等于
,不满足最小值大于等于![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
②当![]() 时,
时,
代数式![]() 取得最大值
取得最大值![]() ,不满足最大值小于等于
,不满足最大值小于等于![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
③当![]() 时,
时,
代数式![]() 取得最大值
取得最大值![]() ,不满足最大值小于等于
,不满足最大值小于等于![]() ,
,
∴![]() 不是线段
不是线段![]() 的封闭代数式.
的封闭代数式.
④当![]() 时,
时,
原式![]()
![]()
![]() ,
,
当![]() 时,
时,
原式![]()
![]()
![]() ,
,
∴![]() ,
,
当![]() 时,
时,
原式![]()
![]()
![]() ,
,
综上所述: ![]() 满足最大值小于等于
满足最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,
,
∴![]() 是线段
是线段![]() 的封闭代数式.
的封闭代数式.
(![]() )当
)当![]() 时,
时,
![]() 取得最大值为
取得最大值为![]() ,
,
则![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
当![]() 时,
时,
![]() 取得最小值为
取得最小值为![]() ,
,
则![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
综上所述: ![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.
点睛:本题考查了信息迁移类题目的解答,用到了数轴上两点间的距离,解绝对值方程等知识点和分类讨论的数学思想;正确理解“封闭代数式”的意义是解答本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某农场300名职工耕种51公顷土地,计划种植水稻,棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 | 每公顷需劳动力 | 每公顷需投入资金 |
水稻 | 4人 | 1万元 |
棉花 | 8人 | 1万元 |
蔬菜 | 5人 | 2万元 |
已知该农场计划在设备上投入67万元,应该怎样安排三种农作物的种植面积,才能使所有的职工都有工作,而且投入的资金正好够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AB=AC,D点在AC上,E点在BA的延长线上,BD=CE,BD的延长线交CE于F.证明: 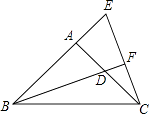
(1)AD=AE
(2)BF⊥CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
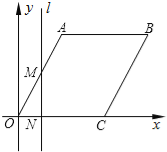
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
A.  B.
B. 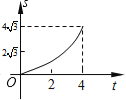
C.  D.
D. 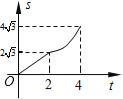
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com