
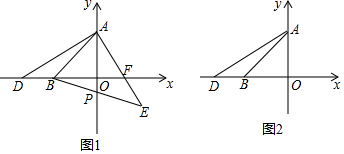
分析 (1)先求出a,b进而得出点A,B坐标,即可得出OA=OB即可;
(2)先判断出点E的横坐标为3,再点P的坐标,进而确定出点E在直线BP上,即可得出点E坐标;
(3)先求出MN,进而求出BM,再求出BD,即可得出结论.
解答 解:(1)∵a2+2ab+b2+(b+3)3=0,
∴(a+b)2+(b+3)3=0,
∴a=3,b=-3,
∴A(0,3),B(-3,0).
∴OA=OB,
∵∠AOB=90°,
∴∠ABO=∠BAO=45°,
(2)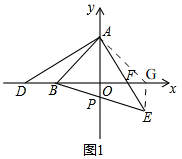 如图1,在OF的延长线取一点G使,OG=OB=3,
如图1,在OF的延长线取一点G使,OG=OB=3,
连接EG,
∴∠AGB=∠ABG=45°,
∴∠BAG=90°,
∵∠DAF=90°,
∴∠BAD=∠GAE,
在△ABD和△AGE中,$\left\{\begin{array}{l}{AB=AG}\\{∠BAD=∠GAF}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△AGE,
∴∠AGE=∠ABD=135°,
∵∠AGB=45°,
∴∠EGB=90°,
∴点E的横坐标为3,
∵OB=3,
∴OP=1,
∴P(0,-1),
∴直线BP的解析式为y=-$\frac{1}{3}$x-1,
∴E(3,-2),
(3)如图2, 过点M作MN⊥AB于N,
过点M作MN⊥AB于N,
在Rt△AMN中,∠MAB=30°,
∴AN=$\sqrt{3}$MN,
在Rt△BMN中,∠ABM=45°,BN=MN,BM=$\sqrt{2}$MN,
在Rt△AOB中,AB=3$\sqrt{2}$,
∴AN+BN=$\sqrt{3}$MN+MN=3$\sqrt{2}$,
∴MN=$\frac{3\sqrt{2}(\sqrt{3}-1)}{2}$,
∴BM=$\sqrt{2}$MN=$\sqrt{2}$×$\frac{3\sqrt{2}(\sqrt{3}-1)}{2}$=3($\sqrt{3}$-1);
在Rt△AOB中,∠ADO=30°,OA=3,
∴OD=3$\sqrt{3}$,
∴BD=OD-OB=3$\sqrt{3}$-3=3($\sqrt{3}$-1),
∴$\frac{BM}{BD}=\frac{3(\sqrt{3}-1)}{3(\sqrt{3}-1)}$=1.
点评 此题是三角形综合题,主要考查了非负性,全等三角形的性质和判定,等腰直角三角形的性质,直角三角形的性质,待定系数法,解本题的关键是判断出点E的横坐标.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
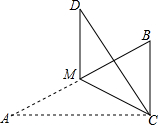 如图,在Rt△ABC中,∠C=90°,∠A<∠B,沿AB边上的中线CM将△ACM翻折,点A落在D处,若BM平分∠CMD,BC=3,则AC的长为( )
如图,在Rt△ABC中,∠C=90°,∠A<∠B,沿AB边上的中线CM将△ACM翻折,点A落在D处,若BM平分∠CMD,BC=3,则AC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 实数x、y在数轴上的对应点的位置如图,把-x、-y、0按照从小到大的顺序排列,正确的是( )
实数x、y在数轴上的对应点的位置如图,把-x、-y、0按照从小到大的顺序排列,正确的是( )| A. | -x<0<y | B. | -y<0<-x | C. | 0<-x<-y | D. | 0<-y<-x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-b<0 | B. | a+1<b-3 | C. | ac2>bc2 | D. | $-\frac{a}{7}<-\frac{b}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.2a吨 | B. | 0.8a吨 | C. | $\frac{5}{6}a$吨 | D. | 0.2a吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | 0.06 | 0.02 | 0.03 | 0.09 |
| A. | 3<x<3.23 | B. | 3.23<x<3.24 | C. | 3.24<x<3.25 | D. | 3.25<x<3.26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com