
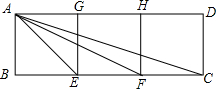
 如图所示,有三个边长为1的小正方形拼成的一个矩形ABCD,∠AEB=
如图所示,有三个边长为1的小正方形拼成的一个矩形ABCD,∠AEB=| AE |
| CE |
| EF |
| AE |
 解:∠AFE+∠ACF=∠AEB.
解:∠AFE+∠ACF=∠AEB.| 12+12 |
| 2 |
| 12+32 |
| 10 |
| 2 |
| 2 |
| 2 |
| AE |
| CE |
| EF |
| AE |
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
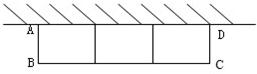 25、如图所示,有一农户用24米长的篱笆围成一面靠墙(墙长为12米)的矩形鸡场ABCD,由大小相等且彼此相连的三个矩形组成,鸡场的总面积为32米2,求出AB边的长.
25、如图所示,有一农户用24米长的篱笆围成一面靠墙(墙长为12米)的矩形鸡场ABCD,由大小相等且彼此相连的三个矩形组成,鸡场的总面积为32米2,求出AB边的长.查看答案和解析>>
科目:初中数学 来源: 题型:044
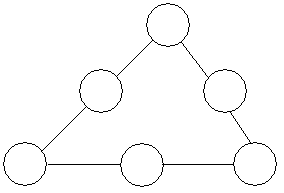
如图所示三角形的三个边长互不相等,现在要将1,2,3,4,5,6这6个数字分别填入3个顶点及每条边的中点的圆圈内,如果要使每条边上的3个数字之和都等于10,那么是否有符合条件的填法?如果有,有多少种不同的填法?如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
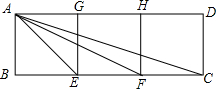 如图所示,有三个边长为1的小正方形拼成的一个矩形ABCD,∠AEB=________,AE=________.请你猜想∠AEB,∠AFE,∠ACF有什么关系,并说明理由.
如图所示,有三个边长为1的小正方形拼成的一个矩形ABCD,∠AEB=________,AE=________.请你猜想∠AEB,∠AFE,∠ACF有什么关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com