练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图7，在正方形ABCD中，E为对角线AC上一点，联结EB、ED，延长BE交AD于点F.

    （1）求证：∠BEC =∠DEC ；

    （2）当CE=CD时，求证：.

    （1）∵四边形ABCD是正方形，∴BC=CD，且∠BCE=∠DCE. ………… (2分)

    又∵CE是公共边，∴△BEC≌△DEC，………………………………………… (2分)

    ∴∠BEC =∠DEC.………………………………………………………………… (1分)

    （2）联结BD .………………………………………………………………………(1分)

    ∵CE=CD,∴∠DEC =∠EDC.…………………………………………………… (1分)

    ∵∠BEC =∠DEC，∠BEC =∠AEF，∴∠EDC=∠AEF.

    ∵∠AEF+∠FED=∠EDC+∠ECD，

    ∴∠FED=∠ECD.………………………………………………………………… (1分)

    ∵四边形ABCD是正方形，

    ∴∠ECD=∠BCD =45°, ∠ADB=∠ADC= 45°，∴∠ECD=∠ADB.… (1分)

    ∴∠FED=∠ADB.  ……………………………………………………………… (1分)

    又∵∠BFD是公共角，∴△FDE∽△FBD，…………………………………… (1分)

    ∴，即. ………………………………………………(1分)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    25、把正方形OFGE纸板按如图①方式放置在正方形纸板ABCD上，顶点G在对角线AC，并把正方形OFGE绕顶点A沿逆时针方向旋转，旋转角为а．
    （1）如图②，当а=90°时，请直接写出线段DE与BF的数量关系和位置关系；
    （2）如图③，当0°＜а＜90°时，（1）中的结论是否发生改变？若不变，请给出证明．若发生改变，请举例说明；
    （3）如图④，将图①、图③中的两个正方形都改为矩形，其他条件不变，设AB=kAD（k＞0），当0°＜а＜90°时，（1）中的结论是否发生改变？若不变，请给出证明．若发生改变，请写出改变后的新结论，并给出证明．

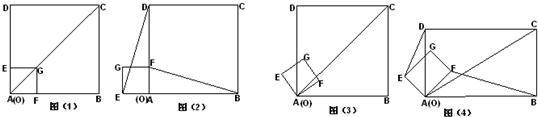
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）填空：如图1，在正方形PQRS中，已知点M、N分别在边QR、RS上，且QM=RN，连接PN、SM相交于点O，则∠POM=
     
    度；
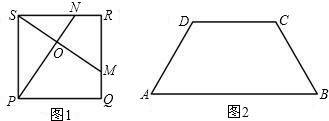    （2）如图2，在等腰梯形ABCD中，已知AB∥CD，BC=CD，∠ABC=60度．以此为部分条件，精英家教网构造一个与上述命题类似的正确命题并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

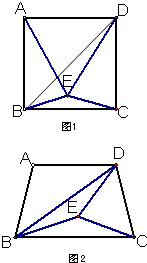    26、如图1，在正方形ABCD中，若点E是△DBC内的一点，且DE=DC，BE=CE．
    （1）连接AE．说明△ABE≌△DCE的理由；
    （2）求∠BDE与∠CDE度数的比值；
    （3）拓展探索：若只将题中的条件“正方形ABCD”换成条件“梯形ABCD中，AD∥BC，AB=DC，2∠DBC=∠DCB”．如图2，研究∠BDE与∠CDE度数的比值是否与（2）中的结论相同，写出你的研究结果并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

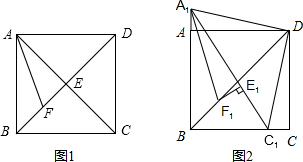    精英家教网如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．
    （1）求证：EF+
    1
    2
    AC=AB；
    （2）点C1从点C出发，沿着线段CB向点B运动（不与点B重合），同时点A1从点A出发，沿着BA的延长线运动，点C1与A1的运动速度相同，当动点C1停止运动时，另一动点A1也随之停止运动．如图2，A1F1平分∠BA1C1，交BD于点F1，过点F1作F1E1⊥A1C1，垂足为E1，请猜想E1F1，
    1
    2
    A1C1与AB三者之间的数量关系，并证明你的猜想；
    （3）在（2）的条件下，当A1E1=3，C1E1=2时，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    课本练习拓展：
    （1）如图1，在正方形ABCD中，E是BC上的一点，△ABE经过旋转后得到△ADF，
    ①旋转中心是点
    A
    A
    ；旋转角度最少是
    90
    90
    度．
    ②爱动脑筋的小兵，在CD边上取点H使得∠HAE=45°，他发现：HE=BE+HD，他的发现正确吗？请你判断并说明理由．
    （2）思维闯关：
    如图2，在直角梯形ABCD中AD∥BC（BC＞AD），∠B=90°BC=AB=6，E是 AB上一点，且∠DCE=45°，BE=2，则DE的长=
    5
    5
    ．（小兵运用解答（1）中所积累的经验和知识做出了该题）
    （3）动手闯过：
    ①小明有一块如图3所示的纸片，其中∠A=∠C=90°，AB=AD．小明请小兵只剪一刀后把它拼成正方形，请你帮助小兵在图中画出剪拼得示意图．
    ②小兵好朋友小红现有两块同小明一样的纸片，如图4，小兵能否在每块上各剪一刀，然后拼成一个大的正方形？若能，请你画出剪法和拼法的示意图；若不能，简要说明理由．

    查看答案和解析>>

    同步练习册答案