
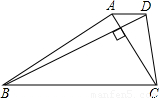
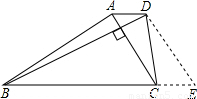
 解:先过D作DE∥AC,交BC的延长线于E,
解:先过D作DE∥AC,交BC的延长线于E,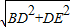 =
=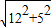 =13,
=13, ×BE=
×BE= ×13=6.5.
×13=6.5.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源:2002年天津市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《三角形》(04)(解析版) 题型:填空题
 ∠DAC;④△ABC是正三角形.请写出正确结论的序号 (把你认为正确结论的序号都填上)
∠DAC;④△ABC是正三角形.请写出正确结论的序号 (把你认为正确结论的序号都填上)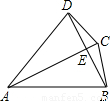
查看答案和解析>>
科目:初中数学 来源:2002年天津市中考数学试卷(解析版) 题型:解答题
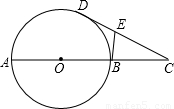
查看答案和解析>>
科目:初中数学 来源:2002年天津市中考数学试卷(解析版) 题型:填空题
 ∠DAC;④△ABC是正三角形.请写出正确结论的序号 (把你认为正确结论的序号都填上)
∠DAC;④△ABC是正三角形.请写出正确结论的序号 (把你认为正确结论的序号都填上)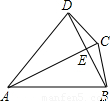
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com