
【题目】点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠FAE=∠FAD,FE=FD.
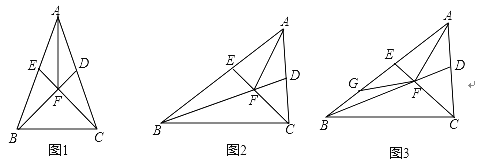
(1)如图1,若∠AEF=∠ADF,求证:AE=AD;
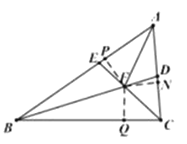
(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;
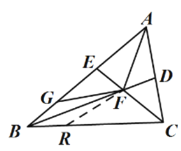
(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明△AEF≌△ADF,根据全等三角形的对应边相等证明结论;
(2)过点F分别作AB,BC,AC边上的高,根据角平分线的性质定理得到FP=FQ,FP=FN,根据角平分线的判定定理得到CF平分∠ACB,证明Rt△PEF≌Rt△NDF,根据全等三角形的性质得到∠PEF=∠FDN,计算得到答案;
(3)在BC上取点R,使CR=CA,分别证明△CAF≌△CRF、△BGF≌△BRF,根据全等三角形的性质、三角形的周长公式计算即可.
(1)∵![]() ,
,![]() ,
,![]() .
.
∴![]() ,∴
,∴![]() .
.

(2)过![]() 点分别作
点分别作![]() ,
,![]() ,
,![]() 边上的高,
边上的高,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 为垂足.
为垂足.
∵![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ,∴
,∴![]() 平分
平分![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.
∴![]() 且
且![]() ,
,
∴![]() .
.
(3)在![]() 上取点
上取点![]() ,使
,使![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]()
![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系内,已知点P(3,3),A(0,b)是y轴上一点,过P作PA的垂线交x轴于B(a,0),则称Q(a,b)为点P的一个关联点。
(1)写出点P的不同的两个关联点的坐标是 、 ;
(2)若点P的关联点Q(x,y)满足5x-3y=14,求出Q点坐标;

(3)已知C(-1,-1)。若点A、点B均在所在坐标轴的正半轴上运动,求△CAB的面积最大值,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线经过A(﹣4,0)、B(0,﹣4)、C(2,0)三点,若点M为第三象限内抛物线上一动点,△AMB的面积为S,则S的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.

(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com