
分析 (1)①当△DEF∽△COD时,$\frac{EF}{OC}=\frac{DE}{DO}$,DF=DEcos∠CDO=$\frac{{3\sqrt{10}}}{5}$,据此求出EF的长度和点F的坐标即可;
②首先以CD为直径作圆,设其圆心为P,交直线a于点Q、Q′,连接PQ,P Q′,由圆周角定理,可得∠CQO=∠CQ′O=∠CDO,在Rt△CDO中,由勾股定理可得CD=$\sqrt{10}$,则PQ=$\frac{1}{2}$CD=$\frac{{\sqrt{10}}}{2}$;然后求出点P的坐标是多少;设Q(-1,a),则($\frac{1}{2}$)2+(a-$\frac{1}{2}$)2=$\frac{5}{2}$,据此求出a的值是多少,进而求出Q点坐标是多少即可;
(2)首先连接OG、OH,判断出△OGH、△OMG均为等腰直角三角形;然后根据△OMG为等腰直角三角形,求出OG的长度,再用OG的长度乘以2,求出AB的长度;最后在直角三角形OAB中,根据OA2+OB2=AB2,求出m的值是多少,进而求出l的函数解析式即可.
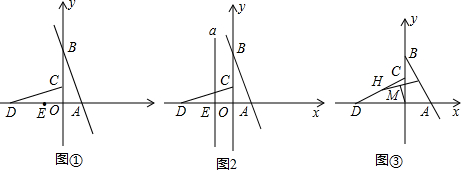
解答 解:(1)①A(1,0),B(0,3),C(0,1),D(-3,0), ,
,
如图1,当△DEF∽△COD时,$\frac{EF}{OC}=\frac{DE}{DO}$,
∴EF=$\frac{2}{3}$,
∴F(-1,$\frac{2}{3}$);
当△DEF∽△COD时,DF=DEcos∠CDO=$\frac{{3\sqrt{10}}}{5}$,
作FK⊥OD于K,
则FK=DFsin∠CDO=$\frac{3}{5}$,DK=DFcos∠CDO=$\frac{9}{5}$,
∴F(-$\frac{6}{5}$,$\frac{3}{5}$);
②如图2,以CD为直径作圆,设其圆心为P,交直线a于点Q、Q′,连接PQ,P Q′, ,
,
由圆周角定理,
可得∠CQO=∠CQ′O=∠CDO,
在Rt△CDO中,由勾股定理可得CD=$\sqrt{10}$,
则PQ=$\frac{1}{2}$CD=$\frac{{\sqrt{10}}}{2}$,
又∵P为CD中点,P($-\frac{3}{2}$,$\frac{1}{2}$),
设Q(-1,a),
则($\frac{1}{2}$)2+(a-$\frac{1}{2}$)2=$\frac{5}{2}$,
解得a=2或-1,
∴Q(-1,2)或(-1,-1).
(2)如图3, ,
,
连接OG、OH,
∵点G为直角三角形OAB的AB边上的中点,
∴OG=$\frac{1}{2}$AB;
∵点H为直角三角形OCD的CD边上的中点,
∴OH=$\frac{1}{2}$CD;
∵AB=CD,OG=$\frac{1}{2}$AB,OH=$\frac{1}{2}$CD,
∴OG=OH,OG⊥OH,
∴△OGH为等腰直角三角形;
∵M为GH中点,
∴OM=OG,OM⊥OG,
∴△OMG为等腰直角三角形,
∴OG=$\sqrt{2}$OM=$\sqrt{2}×\sqrt{10}=2\sqrt{5}$,
∴AB=2OG=2$\sqrt{5}×2$=4$\sqrt{5}$;
∵l:y=mx-4m,
∴A(4,0),B(0,-4m).
因为OA2+OB2=AB2,
所以42+(-4m)2=(4$\sqrt{5}$)2,
解得m=-2或m=2,
根据图示,可得点B的纵坐标大于0,
∴m=-2,-4m=(-4)×(-2)=8,
∴l的函数解析式是:y=-2x+8.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力;
(2)此题还考查了相似三角形的性质,以及函数解析式的求法,要熟练掌握.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
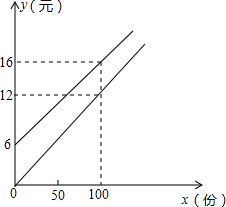 我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
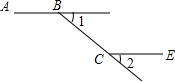 某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前驶到C处,这时他想仍按正东方向行驶,那么他转的方向和角度是向左方向转15度.
某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前驶到C处,这时他想仍按正东方向行驶,那么他转的方向和角度是向左方向转15度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.7 | B. | 6.7<x<6.18 | C. | 6.18<x<6.19 | D. | 6.9<x<9.20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com