
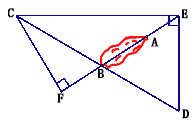
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=![]() .
.
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
【答案】(1) 16.7(海里).(2) ![]() .
.
【解析】
试题分析:(1)在Rt△CED中,利用三角函数求出CE,CD的长,根据中点的定义求得BE的长,AB=BE-AE即可求解;
(2)设BF=x海里.在Rt△CFB中,利用勾股定理求得CF2=CB2-BF2=252-x2=625-x2.在Rt△CFE中,列出关于x的方程,求得x的值,从而求得sin∠BCF的值.
(1)在Rt△CED中,∠CED=90°,DE=30海里,
∴cos∠D=![]() ,
,
∴CE=40(海里),CD=50(海里).
∵B点是CD的中点,
∴BE=![]() CD=25(海里)
CD=25(海里)
∴AB=BE-AE=25-8.3=16.7(海里).
答:小岛两端A、B的距离为16.7海里.
(2)设BF=x海里.
在Rt△CFB中,∠CFB=90°,
∴CF2=CB2-BF2=252-x2=625-x2.
在Rt△CFE中,∠CFE=90°,
∴CF2+EF2=CE2,即625-x2+(25+x)2=1600.
解得x=7.
∴sin∠BCF=![]() .
.
考点: 解直角三角形的应用.


科目:初中数学 来源: 题型:
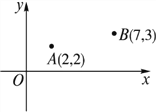
【题目】A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7, 3),根据下列要求作图(保留作图痕迹,不用写作法).
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A,B两校的距离相等?如果有,请用尺规作图找出该点;
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,P点的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
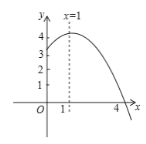
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
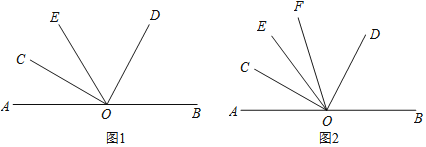
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使∠COD=90°.
(1)如图1,过点O作射线OE,使OE是∠AOD的角平分线,求证:∠BOD=2∠COE;
(2)如图2,过点O作射线OE,使OC是∠AOE的角平分线,另作射线OF,使OF是∠COD的平分线,若∠EOC=3∠EOF,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )
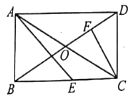
A. ①②B. ②③C. ①②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=x+b与双曲线y=![]() (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(1)求出b、m的值;
(2)点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )

A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 9cm
cm D. 9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:数学课上,老师出示了这祥一个问题:
如图,在正方形ABCD中,点F在AB上,点E在BC延长线上。且AF=CE,连接EF,过点D作DH⊥FE于点H,连接CH并延长交BD于点0,∠BFE=75°.求![]() 的值.某学习小组的同学经过思考,交流了自己的想法:
的值.某学习小组的同学经过思考,交流了自己的想法:
小柏:“通过观察和度量,发现点H是线段EF的中点”。
小吉:“∠BFE=75°,说明图形中隐含着特殊角”;
小亮:“通过观察和度量,发现CO⊥BD”;
小刚:“题目中的条件是连接CH并延长交BD于点O,所以CO平分∠BCD不是己知条件。不能由三线合一得到CO⊥BD”;
小杰:“利用中点作辅助线,直接或通过三角形全等,就能证出CO⊥BD,从而得到结论”;……;
老师:“延长DH交BC于点G,若刪除∠BFB=75°,保留原题其余条件,取AD中点M,连接MH,如果给出AB,MH的值。那么可以求出GE的长度”.
请回答:(1)证明FH=EH;
(2)求![]() 的值;
的值;
(3)若AB=4.MH=![]() ,则GE的长度为_____________.
,则GE的长度为_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com