
【题目】阅读下列材料:
利用完全平方公式,可以将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+11x+24=![]()
=![]()
=![]()
=(x+8)(x+3)
根据以上材料,解析下列问题:
(1)用多项式的配方法将x2+8x﹣1化成(x+m)2+n的形式;
(2)求证:x,y取任何实数时,多项式x2+y2﹣2x﹣4y+16的值总为正数.
科目:初中数学 来源: 题型:
【题目】如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( )

A.50B.44C.38D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用因式分解法解下列方程:
(1)(4x﹣1)(5x+7)=0.
(2)3x(x﹣1)=2﹣2x.
(3)(2x+3)2=4(2x+3).
(4)2(x﹣3)2=x2﹣9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数和反比例函数的图象都经过点 A(3,3).
(1)求正比例函数和反比例函数的解析式;
(2)把直线 OA 向下平移后得到直线 l,与反比例函数的图象交于点 B(6,m),求 m 的值和直线 l 的解 析式;
(3)在(2)中的直线 l 与 x 轴、y 轴分别交于 C、D,求四边形 OABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
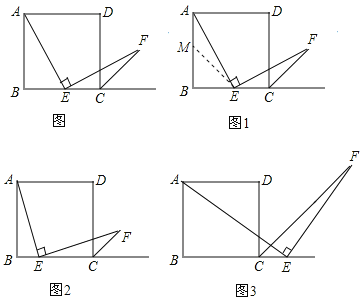
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com