
”¾ĢāÄæ”æijŠ£ĪŖĮĖ¼ÓĒæѧɜµÄ°²Č«ŅāŹ¶£¬×éÖÆѧɜ²Ī¼Ó°²Č«ÖŖŹ¶¾ŗČü£¬²¢“ÓÖŠ³éČ”ĮĖ²æ·ÖѧɜµÄ³É¼Ø£ØµĆ·Ö¾łĪŖÕūŹż£¬Āś·Ö100·Ö£©½ųŠŠĶ³¼Ę£¬»ęÖĘĮĖĮ½·łÉŠ²»ĶźÕūµÄĶ³¼ĘĶ¼ČēĶ¼ĖłŹ¾£¬
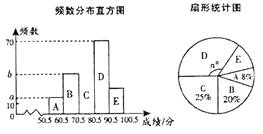
øł¾ŻĶ³¼ĘĶ¼ÖŠµÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Čō![]() ×éµÄʵŹż±Č
×éµÄʵŹż±Č![]() ×銔
×銔![]() £¬ŌņʵŹż·Ö²¼Ö±·½Ķ¼ÖŠ
£¬ŌņʵŹż·Ö²¼Ö±·½Ķ¼ÖŠ![]() ________£¬
________£¬![]() ________£»
________£»
£Ø2£©ÉČŠĪĶ³¼ĘĶ¼ÖŠ![]() ________£¬²¢²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£»
________£¬²¢²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£»
£Ø3£©Čō³É¼ØŌŚ![]() ·ÖŅŌÉĻĪŖÓÅŠć£¬Č«Š£¹²ÓŠ
·ÖŅŌÉĻĪŖÓÅŠć£¬Č«Š£¹²ÓŠ![]() Ćūѧɜ£¬Ēė¹Ą¼Ę³É¼ØÓÅŠćµÄѧɜӊ¶ąÉŁĆū£æ
Ćūѧɜ£¬Ēė¹Ą¼Ę³É¼ØÓÅŠćµÄѧɜӊ¶ąÉŁĆū£æ
”¾“š°ø”æ£Ø1£©16,40£»£Ø2£©![]() £¬¼ū½āĪö£»£Ø3£©¹Ą¼Ę³É¼ØÓÅŠćµÄѧɜӊ470Ćū£®
£¬¼ū½āĪö£»£Ø3£©¹Ą¼Ę³É¼ØÓÅŠćµÄѧɜӊ470Ćū£®
”¾½āĪö”æ
£Ø1£©øł¾ŻČōA×éµÄʵŹż±ČB×銔24£¬ĒŅŅŃÖŖĮ½øö×éµÄ°Ł·Ö±Č£¬¾Ż“Ė¼“æÉĒóµĆ×ÜČĖŹż£¬Č»ŗóøł¾Ż°Ł·Ö±ČµÄŅāŅåĒóµĆa”¢bµÄÖµ£»
£Ø2£©ĄūÓĆ360”ć³ĖŅŌ¶ŌÓ¦µÄ±ČĄż¼“æÉĒó½ā£»
£Ø3£©ĄūÓĆ×ÜČĖŹż³ĖŅŌ¶ŌÓ¦µÄ°Ł·Ö±Č¼“æÉĒó½ā£®
£Ø1£©Ń§Éś×ÜČĖŹż£ŗ![]() £ØČĖ£©
£ØČĖ£©
Ōņ![]() £¬
£¬![]()
£Ø2£©![]() £¬
£¬
![]() ×éµÄČĖŹżŹĒ£ŗ
×éµÄČĖŹżŹĒ£ŗ![]() £ØČĖ£©£¬²¹Č«ĢõŠĪĶ³¼ĘĶ¼ČēĶ¼
£ØČĖ£©£¬²¹Č«ĢõŠĪĶ³¼ĘĶ¼ČēĶ¼
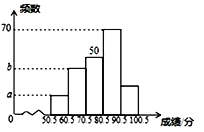
£Ø3£©Ńł±¾![]() ”¢
”¢![]() Į½×éµÄ°Ł·ÖŹżµÄŗĶĪŖ
Į½×éµÄ°Ł·ÖŹżµÄŗĶĪŖ![]() £¬
£¬
”ą![]() £ØĆū£©
£ØĆū£©
“š£ŗ¹Ą¼Ę³É¼ØÓÅŠćµÄѧɜӊ470Ćū£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«Ņ»ÕžŲŠĪÖ½Ę¬ABCDŃŲ¶Ō½ĒĻßBDÕŪµž£¬µćCµÄ¶ŌÓ¦µćĪŖC”䣬ŌŁ½«ĖłÕŪµĆµÄĶ¼ŠĪŃŲEFÕŪµž£¬Ź¹µĆµćDŗĶµćAÖŲŗĻ£®ČōAB=3£¬BC=4£¬ŌņÕŪŗŪEFµÄ³¤ĪŖ__________£®
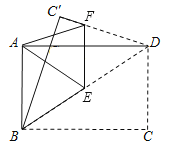
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ŌĶĮĻĀĆę²ÄĮĻ£ŗ
µćA”¢BŌŚŹżÖįÉĻ·Ö±š±ķŹ¾ŹµŹża”¢b£¬A”¢BĮ½µćÖ®¼äµÄ¾ąĄė±ķŹ¾ĪŖ|AB|£®µ±A”¢BĮ½µćÖŠÓŠŅ»µćŌŚŌµćŹ±£¬²»·ĮÉčµćAŌŚŌµć£¬ČēĶ¼1£¬|AB|£½|OB|£½|b|£½|a©b|£»µ±A”¢BĮ½µć¶¼²»ŌŚŌµćŹ±£¬
¢ŁČēĶ¼2£¬µćA”¢B¶¼ŌŚŌµćµÄÓŅ±ß|AB|£½|OB|©|OA|£½|b|©|a|£½b©a£½|a©b|£»
¢ŚČēĶ¼3£¬µćA”¢B¶¼ŌŚŌµćµÄ×ó±ß£¬|AB|£½|OB|©|OA|£½|b|©|a|£½©b©£Ø©a£©£½|a©b|£»
¢ŪČēĶ¼4£¬µćA”¢BŌŚŌµćµÄĮ½±ß£¬|AB|£½|OB|+|OA|£½|a|+|b|£½a+£Ø©b£©£½|a©b|

£Ø2£©»Ų“šĻĀĮŠĪŹĢā£ŗ
¢ŁŹżÖįÉĻ±ķŹ¾2ŗĶ5µÄĮ½µćÖ®¼äµÄ¾ąĄėŹĒ”” ””£¬ŹżÖįÉĻ±ķŹ¾©2ŗĶ©5µÄĮ½µćÖ®¼äµÄ¾ąĄėŹĒ”” ””£¬ŹżÖįÉĻ±ķŹ¾1ŗĶ©3µÄĮ½µćÖ®¼äµÄ¾ąĄėŹĒ”” ””£»
¢ŚŹżÖįÉĻ±ķŹ¾xŗĶ©1µÄĮ½µćAŗĶBÖ®¼äµÄ¾ąĄėŹĒ”” ””£¬Čē¹ū|AB|£½2£¬ÄĒĆ“xĪŖ”” ””£»
¢Ū“śŹżŹ½|x+1|+|x©2|Č”×īŠ”ÖµŹ±£¬ĻąÓ¦µÄÕūŹżxµÄȔֵŹĒ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
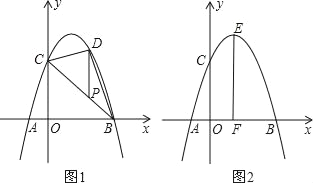
”¾ĢāÄæ”æÅ×ĪļĻßy=©x2+bx+c¾¹żµćA”¢B”¢C£¬ŅŃÖŖA£Ø©1£¬0£©£¬C£Ø0£¬3£©£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ČēĶ¼1£¬PĪŖĻ߶ĪBCÉĻŅ»µć£¬¹żµćP×÷yÖįĘ½ŠŠĻߣ¬½»Å×ĪļĻßÓŚµćD£¬µ±”÷BDCµÄĆ껿×ī“óŹ±£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£¬Å×ĪļĻ߶„µćĪŖE£¬EF”ĶxÖįÓŚFµć£¬M£Øm£¬0£©ŹĒxÖįÉĻŅ»¶Æµć£¬NŹĒĻ߶ĪEFÉĻŅ»µć£¬Čō”ĻMNC=90”ć£¬ĒėÖø³öŹµŹżmµÄ±ä»Æ·¶Ī§£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ³¤·½ŠĪABCDÖŠ£¬µćMĪŖCDÖŠµć£¬½«”÷MBCŃŲBM·ÕŪÖĮ”÷MBE£¬Čō”ĻAME £½ ¦Į£¬”ĻABE £½ ¦Ā£¬Ōņ ¦Į Óė ¦Ā Ö®¼äµÄŹżĮæ¹ŲĻµĪŖ( )
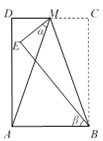
A. ¦Į£«3¦Ā£½180”ć B. ¦Ā£¦Į£½20”ć C. ¦Į£«¦Ā£½80”ć D. 3¦Ā£2¦Į£½90”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬µćCŌŚ”ŃOÉĻ£¬”ĻABCµÄĘ½·ÖĻßÓėACĻą½»ÓŚµćD£¬Óė”ŃO¹żµćAµÄĒŠĻßĻą½»ÓŚµćE£®
£Ø1£©”ĻACB=”” ”””ć£¬ĄķÓÉŹĒ£ŗ”” ””£»
£Ø2£©²ĀĻė”÷EADµÄŠĪד£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£»
£Ø3£©ČōAB=8£¬AD=6£¬ĒóBD£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ļ߶ĪABŗĶCDŹżÖįÉĻŌĖ¶Æ£¬AæŖŹ¼Ź±ÓėŌµćÖŲŗĻ£¬ĒŅ![]() .
.
(1)ČōAB=10£¬ĒŅBĪŖĻ߶ĪACµÄÖŠµć£¬ĒóĻ߶ĪADµÄ³¤.
(2)ŌŚ(1)µÄĢõ¼žĻĀ£¬Ļ߶ĪABŗĶCDĶ¬Ź±æŖŹ¼ĻņÓŅŌĖ¶Æ£¬Ļ߶ĪABµÄĖŁ¶ČĪŖ5øöµ„Ī»/Ćė£¬Ļ߶ĪCDµÄĖŁ¶ČĪŖ3øöµ„Ī»/Ćė£¬¾¹żtĆėĒ”ŗĆÓŠ![]() £¬ĒótµÄÖµ.
£¬ĒótµÄÖµ.
(3)ČōĻ߶ĪABŗĶCDĶ¬Ź±æŖŹ¼Ļņ×óŌĖ¶Æ£¬ĒŅĻ߶ĪABµÄĖŁ¶Č“óÓŚĻ߶ĪCDµÄĖŁ¶Č£¬ŌŚµćAŗĶCÖ®¼äÓŠŅ»µćP(²»ÓėµćBÖŲŗĻ)£¬ĒŅÓŠ![]() £¬“ĖŹ±Ļ߶ĪBPĪŖ¶ØÖµĀš£æČōŹĒĒėĒó³öÕāøö¶ØÖµ£¬Čō²»ŹĒĒėĖµĆ÷ĄķÓÉ.
£¬“ĖŹ±Ļ߶ĪBPĪŖ¶ØÖµĀš£æČōŹĒĒėĒó³öÕāøö¶ØÖµ£¬Čō²»ŹĒĒėĖµĆ÷ĄķÓÉ.
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷ĆæĢģŌēÉĻŅŖŌŚ7£ŗ50Ö®Ē°øĻµ½¾ą¼Ņ900Ć×µÄѧŠ£ÉĻѧ.Š”Ć÷ŅŌ60Ć×/·ÖµÄĖŁ¶Č³ö·¢10·Öŗ󣬊”Ć÷µÄ°Ö°Ö·¢ĻÖĖūĶüĮĖ“ųÓļĪÄŹé.ÓŚŹĒ£¬°Ö°ÖĮ¢¼“ŅŌ160Ć×/·ÖµÄĖŁ¶ČȄ׷Š”Ć÷£¬°Ö°ÖÄÜ·ńŌŚŠ”Ć÷½ųѧŠ£Ē°×·ÉĻĖū£æČōÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£¬Čō²»ÄÜ£¬Ēė¼ĘĖć£¬°Ö°ÖµÄĖŁ¶ČÖĮÉŁĪŖ¶ąÉŁŹ±²ÅÄÜøĻŌŚŠ”Ć÷½ųѧŠ£Ē°×·ÉĻĖū£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
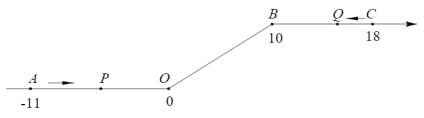
”¾ĢāÄæ”æČēĶ¼£¬½«Ņ»ĢõŹżÖįŌŚŌµćOŗĶµćB“¦ø÷ÕŪŅ»ĻĀ£¬µĆµ½Ņ»Ģõ ”°ÕŪĻߏżÖį”± £®Ķ¼ÖŠµćA±ķŹ¾£11£¬µćB±ķŹ¾10£¬µćC±ķŹ¾18£¬ĪŅĆĒ³ĘµćAŗĶµćCŌŚŹżÖįÉĻĻą¾ą29øö³¤¶Čµ„Ī»£®¶ÆµćP“ÓµćA³ö·¢£¬ŅŌ2µ„Ī»/ĆėµÄĖŁ¶ČŃŲ×Å”°ÕŪĻߏżÖį”±µÄÕż·½ĻņŌĖ¶Æ£¬“ÓµćOŌĖ¶Æµ½µćBĘŚ¼äĖŁ¶Č±äĪŖŌĄ“µÄŅ»°ė£¬Ö®ŗóĮ¢æĢ»Öø“ŌĖŁ£»Ķ¬Ź±£¬¶ÆµćQ“ÓµćC³ö·¢£¬ŅŌ1µ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅŹżÖįµÄøŗ·½ĻņŌĖ¶Æ£¬“ÓµćBŌĖ¶Æµ½µćOĘŚ¼äĖŁ¶Č±äĪŖŌĄ“µÄĮ½±¶£¬Ö®ŗóŅ²Į¢æĢ»Öø“ŌĖŁ£®ÉčŌĖ¶ÆµÄŹ±¼äĪŖtĆė£®
ĪŹ£ŗ£Ø1£©¶ÆµćP“ÓµćAŌĖ¶ÆÖĮCµćŠčŅŖ¶ąÉŁŹ±¼ä£æ
£Ø2£©P”¢QĮ½µćĻąÓöŹ±£¬Ēó³öĻąÓöµćMĖł¶ŌÓ¦µÄŹżŹĒ¶ąÉŁ£»
£Ø3£©Ēóµ±tĪŖŗĪÖµŹ±£¬P”¢BĮ½µćŌŚŹżÖįÉĻĻą¾ąµÄ³¤¶ČÓėQ”¢OĮ½µćŌŚŹżÖįÉĻĻą¾ąµÄ³¤¶ČĻąµČ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com