
【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
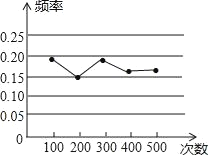
A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校![]() 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.

(1)![]() _____________,
_____________,![]() _______________;
_______________;
(2)请补全上图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;
(4)在抽查的![]() 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
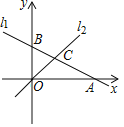
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+![]() 与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.

(1)如图1,求抛物线的顶点坐标;
(2)如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ⊥AC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式;
(3)在(2)的条件下,如图3,连接AP,过点C作CE⊥AP于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
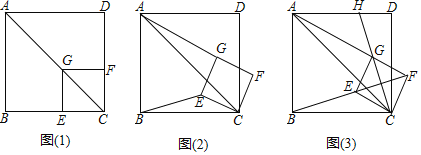
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,GF⊥CD.
(1)①求证:四边形CEGF是正方形;②推断:![]() 的值为 :
的值为 :
(2)将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系;
(3)正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,求正方形CEGF和正方形ABCD的边长.
,求正方形CEGF和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
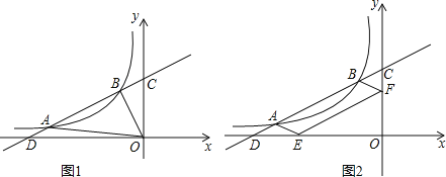
【题目】 如图,一次函数y=0.5x+3的图象与反比例函数y=![]() (k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(1)求此反比例函数的表达式和B点坐标;
(2)连接AO和BO,若点P在x轴上,且S△BDP=![]() S△BOA,求点P的坐标;
S△BOA,求点P的坐标;
(3)如图2,作ABFE,点F和点E分别在y轴和x轴上,求证:∠AED=∠FEO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com