
 如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积$\frac{7\sqrt{3}}{2}$.
如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积$\frac{7\sqrt{3}}{2}$. 分析 如图1,作CK⊥AB于K,过E点作EP⊥BC于P.想办法求出CK、EP、EC,再证明△BCE≌△GCF(ASA)推出CE=CF,根据三角形的面积公式计算即可.
解答 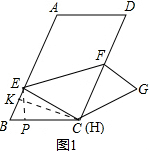 解:如图1,作CK⊥AB于K,过E点作EP⊥BC于P.
解:如图1,作CK⊥AB于K,过E点作EP⊥BC于P.
∵∠B=60°,
∴CK=BC•sin60°=4×$\frac{\sqrt{3}}{2}$=2 $\sqrt{3}$,
∵C到AB的距离和E到CD的距离都是平行线AB、CD间的距离,
∴点E到CD的距离是2 $\sqrt{3}$,
∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠A=∠BCD,
由折叠可知,AD=CG,∠D=∠G,∠A=∠ECG,
∴BC=GC,∠B=∠G,∠BCD=∠ECG,
∴∠BCE=∠GCF,
在△BCE和△GCF中,
$\left\{\begin{array}{l}{∠B=∠G}\\{∠BCE=∠GCF}\\{BC=GC}\end{array}\right.$,
∴△BCE≌△GCF(ASA);
∴CE=CF,
∵∠B=60°,∠EPB=90°,
∴∠BEP=30°,
∴BE=2BP,
设BP=m,则BE=2m,
∴EP=BE•sin60°=2m×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$m,
由折叠可知,AE=CE,
∵AB=6,
∴AE=CE=6-2m,
∵BC=4,
∴PC=4-m,
在Rt△ECP中,由勾股定理得(4-m)2+( $\sqrt{3}$-m)2=(6-2m)2,解得m=$\frac{5}{4}$,
∴EC=6-2m=6-2×$\frac{5}{4}$=$\frac{7}{2}$,
∴CF=EC=$\frac{7}{2}$,
∴S△CEF=$\frac{1}{2}$×$\frac{7}{2}$×2 $\sqrt{3}$=$\frac{7\sqrt{3}}{2}$,
故答案为$\frac{7\sqrt{3}}{2}$.
点评 本题是四边形综合题,考查了解直角三角形,平行四边形的性质,折叠的性质勾股定理的应用,三角形相似的判定和性质,三角形面积等,熟练掌握性质定理是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y=mx(m为常数,且m≠0)与双曲线y=$\frac{k}{x}$(k为常数,且k≠0)相交于A(-2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为12.
如图,直线y=mx(m为常数,且m≠0)与双曲线y=$\frac{k}{x}$(k为常数,且k≠0)相交于A(-2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
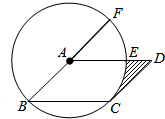 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com