
分析 由a2+b2=4ab,先求出(a+b)和(a-b)的平方,再求出其算术平方根进行计算即可.
解答 解:∵由a2+b2=4ab,
∴(a+b)2=6ab①,(a-b)2=2ab②,
∵a>b>0,
∴a+b=$\sqrt{6ab}$,a-b=$\sqrt{2ab}$,
∴原式=$\frac{{b}^{2}-{a}^{2}}{ab}$=$\frac{-{(a}^{2}-{b}^{2})}{ab}$=-$\frac{(a+b)(a-b)}{ab}$=-$\frac{\sqrt{6ab}•\sqrt{2ab}}{ab}$=-2$\sqrt{3}$.
故答案为:-2$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,直线AB经过⊙O上的点C,OA与⊙O 交于点D,若OA=OB,AD=CD,∠A=30°
已知:如图,直线AB经过⊙O上的点C,OA与⊙O 交于点D,若OA=OB,AD=CD,∠A=30°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
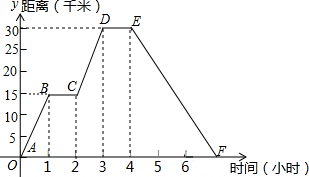 小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 张老师为了激发学生的学习兴趣,设计一个“配紫色”游戏.如图是两个可以自由转动的转盘,每个转盘被分成大小相等的几个扇形.转盘甲中的扇形分别涂有红、蓝、白三种颜色,转盘乙中的扇形分别涂有黄、绿、蓝、红四种颜色.游戏者同时转动两个转盘,如果转盘停止后,一个转盘的指针指向红色,另一个转盘的指针指向蓝色,那么红色和蓝色在一起就配成了紫色(若指针指向扇形的分界线,则需重新转动).
张老师为了激发学生的学习兴趣,设计一个“配紫色”游戏.如图是两个可以自由转动的转盘,每个转盘被分成大小相等的几个扇形.转盘甲中的扇形分别涂有红、蓝、白三种颜色,转盘乙中的扇形分别涂有黄、绿、蓝、红四种颜色.游戏者同时转动两个转盘,如果转盘停止后,一个转盘的指针指向红色,另一个转盘的指针指向蓝色,那么红色和蓝色在一起就配成了紫色(若指针指向扇形的分界线,则需重新转动).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com