
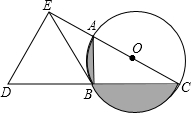
 如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.分析 (1)连接BO,根据△OBC和△BCE都是等腰三角形,即可得到∠BEC=∠OBC=∠OCB=30°,再根据三角形内角和即可得到∠EBO=90°,进而得出BE是⊙O的切线;
(2)在Rt△ABC中,根据∠ACB=30°,BC=3,即可得到半圆的面积以及Rt△ABC的面积,进而得到阴影部分的面积.
解答 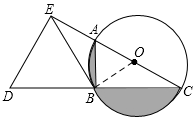 解:(1)如图所示,连接BO,
解:(1)如图所示,连接BO,
∵∠ACB=30°,
∴∠OBC=∠OCB=30°,
∵DE⊥AC,CB=BD,
∴Rt△DCE中,BE=$\frac{1}{2}$CD=BC,
∴∠BEC=∠BCE=30°,
∴△BCE中,∠EBC=180°-∠BEC-∠BCE=120°,
∴∠EBO=∠EBC-∠OBC=120°-30°=90°,
∴BE是⊙O的切线;
(2)当BE=3时,BC=3,
∵AC为⊙O的直径,
∴∠ABC=90°,
又∵∠ACB=30°,
∴AB=tan30°×BC=$\sqrt{3}$,
∴AC=2AB=2$\sqrt{3}$,AO=$\sqrt{3}$,
∴阴影部分的面积=半圆的面积-Rt△ABC的面积=$\frac{1}{2}$π×AO2-$\frac{1}{2}$AB×BC=$\frac{1}{2}$π×3-$\frac{1}{2}$×$\sqrt{3}$×3=$\frac{3}{2}π$-$\frac{3}{2}\sqrt{3}$.
点评 本题主要考查了切线的判定以及扇形面积的计算,解题时注意:经过半径的外端且垂直于这条半径的直线是圆的切线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
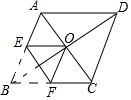 如图,菱形ABCD的对角线相交于点O,AC=2,BD=2$\sqrt{3}$,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为7.
如图,菱形ABCD的对角线相交于点O,AC=2,BD=2$\sqrt{3}$,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
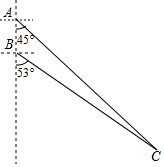 如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,$\sqrt{2}$≈1.41)
如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
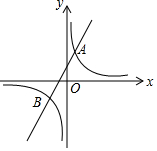 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com