
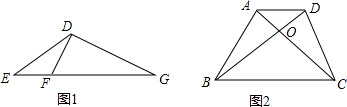
| A. | (2)(3) | B. | (1)(3)(4) | C. | (1)(2)(3)(4) | D. | (1)(3) |
分析 (1)根据比例中项的定义即可求解;
(2)根据比例的基本性质,a:b=b:c依此即可求解;
(3)根据AA可得△DEF∽△GED,根据相似三角形的性质和比例中项的定义即可求解;
(4)根据AD∥BC得到△AOD∽△COB,可得相似三角形相似比,再利用同高的三角形面积比等于底边比,可求面积比,再根据比例中项的定义即可求解.
解答 解:(1)若a,b,c满足$\frac{a}{b}$=$\frac{b}{c}$,则b2=ac,b是a,c的比例中项,符合题意;
(2)依题意有b2=2×8,
解得b=±4,不符合题意;
(3)∵∠EDF=∠G,∠E=∠E,
∴△DEF∽△GED,
∴EF:DE=DE:EG,
∴DE2=EF•EG,
∴DE是EF,EG的比例中项,符合题意;
(4)∵AD∥BC,
∴△AOD∽△COB,
∴OA:OC=AD:BC=OD:OB,
∴S1:S2=OD:OB,
同理S2:S3=OA:OC=OD:OB,
∴S1:S2=S2:S3,
∴S1•S3=S22,则S2是S1、S3的比例中项,符合题意.
故选B.
点评 考查了比例线段,理解比例中项的概念:当比例式中的两个内项相同时,即叫比例中项.根据比例的基本性质进行计算.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
| 节水量/立方米 | 1 | 1.5 | 2.5 | 3 |
| 户数/户 | 50 | 80 | a | 70 |

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5×1011 千克 | B. | 50×109 千克 | C. | 5×109 千克 | D. | 5×1010 千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 25 | 29 | 32 | 34 | 35 | 38 | 40 |
| 人数(人) | 2 | 4 | 3 | 7 | 9 | 7 | 6 |
| A. | 该班一共有38名同学 | |
| B. | 该班学生这次考试成绩的众数是35分 | |
| C. | 该班学生这次考试成绩的中位数是35分 | |
| D. | 该班学生这次考试成绩的平均数是35分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
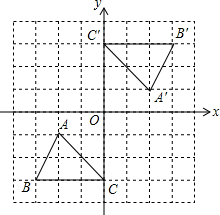 如图,已知格点△ABC和△A′B′C′关于原点O成中心对称,在方格网中确定一点D,使以A,O,C′,D为顶点的四边形是平行四边形,则点D的坐标为(2,4)或(-2,-4)或(-2,2)(请写出所有满足条件的点D的坐标)
如图,已知格点△ABC和△A′B′C′关于原点O成中心对称,在方格网中确定一点D,使以A,O,C′,D为顶点的四边形是平行四边形,则点D的坐标为(2,4)或(-2,-4)或(-2,2)(请写出所有满足条件的点D的坐标)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com