

| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -1 | 3 | 5 | 5 | … |
分析 (1)如图1,作NH⊥OC于H,设OQ=x,则OM=4x,MC=2x,先判断四边形OQPM为平行四边形得到PQ=OM=4x,再证明△NQP∽△NOC,利用相似比得到NQ=2x,接着在Rt△NOH中利用含30度的直角三角形三边的关系得到OH=$\frac{3}{2}$x,NH=$\frac{3\sqrt{3}}{2}$x,则CH=$\frac{9}{2}$x,则利用勾股定理可计算出CN=3$\sqrt{3}$x,从而得到ON:CN:OC的比值;
(2)如图2,先证明四边形OQPM为菱形得到PQ=PM=OM,再证明△NQP∽△NOC,利用比例线段得到$\frac{OM}{OC}$=$\frac{NP}{NC}$①,同理可得$\frac{OM}{ON}$=$\frac{CP}{NC}$②,则把①与②相加得$\frac{OM}{OC}$+$\frac{OM}{ON}$=1,从而得到$\frac{1}{OM}$-$\frac{1}{ON}$=$\frac{1}{m}$,所以判断$\frac{1}{OM}$-$\frac{1}{ON}$的值随m的变化而发生变化;
(3)利用待定系数法确定抛物线解析式为y=-x2+3x+3,则关于x的方程ax2+(b-1)x+c=0化为-x2+2x+3=0,解方程得到m=3,作PE⊥OB于E,PF⊥OA于F,如图2,根据角平分线性质得到PE=PF,再利用菱形的面积公式和三角形面积公式得到S1=OM•PF,S2=$\frac{1}{2}$•PF•(ON+OC),所以$\frac{{S}_{1}}{{S}_{2}}$=$\frac{OM}{\frac{1}{2}(ON+3)}$,设$\frac{{S}_{1}}{{S}_{2}}$=t,则$\frac{OM}{\frac{1}{2}(ON+3)}$=t,用OM和t表示出ON,再代入$\frac{1}{OM}$-$\frac{1}{ON}$=$\frac{1}{3}$得$\frac{1}{OM}$-$\frac{t}{2OM-3t}$=$\frac{1}{3}$,整理得关于OM的一元二次方程2OM2-6OM+9t=0,然后利用判别式的意义可确定t的范围.
解答 解:(1)ON:CN:OC=1:$\sqrt{3}$:2.理由如下:
如图1,作NH⊥OC于H,
设OQ=x,则OM=4x,MC=2x,
∵PQ∥OC,PM∥OB,
∴四边形OQPM为平行四边形,
∴PQ=OM=4x,
∵PQ∥OC,
∴△NQP∽△NOC,
∴$\frac{NQ}{NO}$=$\frac{QP}{OC}$,即$\frac{NQ}{NQ+x}$=$\frac{4x}{4x+2x}$,解得NQ=2x,
在Rt△NOH中,∵∠O=60°,
∴OH=$\frac{1}{2}$ON=$\frac{3}{2}$x,NH=$\sqrt{3}$OH=$\frac{3\sqrt{3}}{2}$x,
∴CH=OC-OH=6x-$\frac{3}{2}$x=$\frac{9}{2}$x,
在Rt△NHC中,CN=$\sqrt{(\frac{3\sqrt{3}}{2}x)^{2}+(\frac{9}{2}x)^{2}}$=3$\sqrt{3}$x,
∴ON:CN:OC=3x:3$\sqrt{3}$x:6x=1:$\sqrt{3}$:2;
(2)$\frac{1}{OM}$-$\frac{1}{ON}$的值发生变化,$\frac{1}{OM}$-$\frac{1}{ON}$=$\frac{1}{m}$.
如图2,
∵OP平分∠AOB,
∴∠AOP=∠BOP,
而PQ∥OC,
∴∠AOP=∠QPO,
∴∠QPO=∠BOP,
∴QO=QP,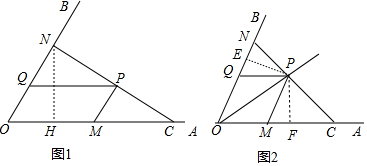
∴四边形OQPM为菱形,
∴PQ=PM=OM,
∵PQ∥OC,
∴△NQP∽△NOC,
∴$\frac{PQ}{OC}$=$\frac{NP}{NC}$,即$\frac{OM}{OC}$=$\frac{NP}{NC}$①,
∵PM∥ON,
∴△CPM∽△CNO,
∴$\frac{PM}{ON}$=$\frac{CP}{NC}$,即$\frac{OM}{ON}$=$\frac{CP}{NC}$②,
①+②得$\frac{OM}{OC}$+$\frac{OM}{ON}$=$\frac{NP}{NC}$+$\frac{CP}{NC}$=1,
∴$\frac{1}{OC}$+$\frac{1}{ON}$=$\frac{1}{OM}$,
∴$\frac{1}{OM}$-$\frac{1}{ON}$=$\frac{1}{m}$;
(3)把(0,3)、(-1,-1),(1,5)代入y=ax2+bx+c得$\left\{\begin{array}{l}{c=3}\\{a-b+c=-1}\\{a+b+c=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2+3x+3,
关于x的方程ax2+(b-1)x+c=0化为-x2+2x+3=0,解得x1=-1,x2=3,
∴m=3,
作PE⊥OB于E,PF⊥OA于F,如图2,则PE=PF,
∴S1=OM•PF,S2=$\frac{1}{2}$PE•ON+$\frac{1}{2}$PF•OC=$\frac{1}{2}$•PF•(ON+OC)
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{OM}{\frac{1}{2}(ON+3)}$,
设$\frac{{S}_{1}}{{S}_{2}}$=t,则$\frac{OM}{\frac{1}{2}(ON+3)}$=t,
∴ON=$\frac{2OM-3t}{t}$,
∵$\frac{1}{OM}$-$\frac{1}{ON}$=$\frac{1}{3}$,
∴$\frac{1}{OM}$-$\frac{t}{2OM-3t}$=$\frac{1}{3}$,
整理得2OM2-6OM+9t=0,
△=62-4×2×9t≥0,解得t≤$\frac{1}{2}$,
∴0<$\frac{{S}_{1}}{{S}_{2}}$≤$\frac{1}{2}$.
点评 本题考查了二次函数的综合题:熟练掌握角平分线的性质、平行四边形的判定与性质、菱形的判定与性质和比例的性质;会利用待定系数法求二次函数解析式;灵活应用相似比和勾股定理进行几何计算;会利用判别式解决最值问题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
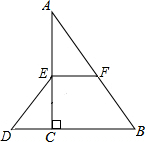 如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.
如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
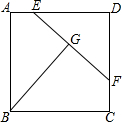 如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.
如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
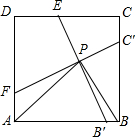 如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.
如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )| A. | 16$\sqrt{3}$ | B. | 32 | C. | 8$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x-1-6=2(3x+1) | B. | (x-1)-1=2(x+1) | C. | 3(x-1)-1=2(3x+1) | D. | 3(x-1)-6=2(3x+1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com