
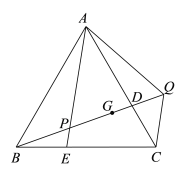
【题目】如图,在等边△ABC中,点D是AC上的一点,在BC上取一点E,使BE=CD,连接AE交BD于点P,在BD的延长线上取一点Q,使AP=PQ,连接AQ、CQ,点G为PQ的中点,DG=PE,若CQ=![]() ,则BQ=________________.
,则BQ=________________.
【答案】![]()
【解析】
如下图,连接CG,由已知条件易证△ABE≌△BCD,由此可得∠BAE=∠CBD,从而可得∠APQ=∠BAE+∠ABP=∠ABC=60°,结合AP=PQ可得△APQ是等边三角形,由此易证△ABP≌△ACQ,从而可得BP=CQ=![]() ,再通过证∠BEP=∠CDG,证得△BEP≌△CDG可得CG=BP=CQ,∠CGD=∠BPE=∠APD=60°,由此可得△CGQ是等边三角形,由此可得GQ=CQ=
,再通过证∠BEP=∠CDG,证得△BEP≌△CDG可得CG=BP=CQ,∠CGD=∠BPE=∠APD=60°,由此可得△CGQ是等边三角形,由此可得GQ=CQ=![]() ,结合点G是PQ的中点可得PQ=
,结合点G是PQ的中点可得PQ=![]() ,由此即可得到BQ=
,由此即可得到BQ=![]() .
.
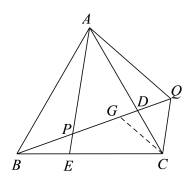
如下图,连接CQ,∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠BCD=60°,
∵BE=CD,
∴△ABE≌△BCD,
∴∠BAE=∠CBD,
∴∠APQ=∠BAE+∠ABD=∠CBD+∠ABD=∠ABC=60°,
∵AP=PQ,
∴△APQ是等边三角形,
∴∠PAQ=∠BAC=60°,AP=AQ,
∴∠BAC-∠EAC=∠PAQ-∠EAC,即∠BAP=∠CAQ,
∴△BAP≌△CAQ,
∴BP=CQ=![]() ,
,
∵∠BEP=∠ACB+∠CAE=60°+∠CAE,∠CDG=∠APQ+∠CAE=60°+∠CAE,
∴∠BEP=∠CDG,
又∵BE=CD,PE=DG,
∴△BEP≌△CDG,
∴CG=BP=CQ,∠PBE=∠GCD,
∴∠DGC=∠PBE+∠GCB=∠GCD+∠GCB=∠DCB=60°,
∴△GCD是等边三角形,
∴GQ=CQ=![]() ,
,
又∵点G是PQ的中点,
∴PQ=2GQ=![]() ,
,
∴BQ=BP+PQ=![]() .
.
故答案为:![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于B,与直线y=x交于点C.
与x轴交于点A,与y轴交于B,与直线y=x交于点C.
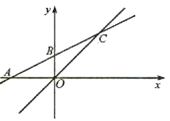
(1)求A、B、C三点的坐标;
(2)求△AOC的面积;
(3)已知点P是x轴正半轴上的一点,若△COP是等腰三角形,直接写点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
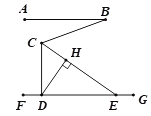
【题目】如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH=________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用500元购进钢笔若干支,第二次又用500元购进该款钢笔,但这次每支的进价是第一次进价的 ![]() 倍,购进数量比第一次少了25支.
倍,购进数量比第一次少了25支.
(1)求第一次每支钢笔的进价是多少元?
(2)若要求这两次购进的钢笔按同一价格全部销售完毕后获利不低于350元,问每支售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)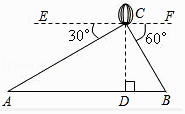
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南昌的雾霾引起了小张对环保问题的重视.一次旅游小张思考了一个问题.从某地到南昌,若乘火车需要![]() 小时,若乘汽车需要
小时,若乘汽车需要![]() 小时.这两种交通工具平均每小时二氧化碳的排放量之和为
小时.这两种交通工具平均每小时二氧化碳的排放量之和为![]() 千克,火车全程二氧化碳的排放总量比汽车的多
千克,火车全程二氧化碳的排放总量比汽车的多![]() 千克,分别求火车和汽车平均每小时二氧化碳的排放量.
千克,分别求火车和汽车平均每小时二氧化碳的排放量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距70千米,甲从A地出发,每小时行15千米,乙从B地出发,每小时行20千米.
(1)若两人同时出发,相向而行,则经过几小时两人相遇?
(2)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10千米?
(3)若两人同时出发,相向而行,则几小时后两人相距10千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“在线教育”指的是通过应用信息科技和互联网技术进行内容传播和快速学习的方法.“互联网+”时代,中国的在线教育得到迅猛发展. 请根据下面张老师与记者的对话内容,求2014年到2016年中国在线教育市场产值的年平均增长率.
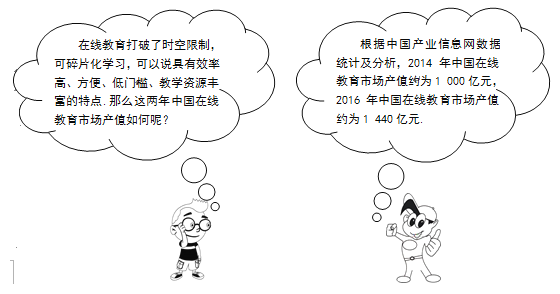
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
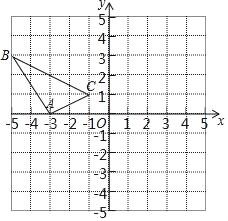
【答案】(1)画图见解析;(2)(0,2).
【解析】
(1)根据中心对称和平移性质分别作出变换后三顶点的对应点,再顺次连接可得;
(2)根据中心对称的概念即可判断.
(1)如图所示,△A1B1C1和△A2B2C2即为所求;
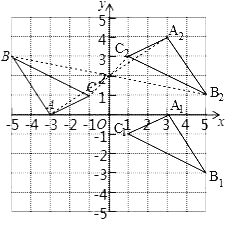
(2)由图可知,△A2B2C2与△ABC关于点(0,2)成中心对称.
点睛:本题考查了中心对称作图和平移作图,熟练掌握中心对称的性质和平移的性质是解答本题的关键. 中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
【题型】解答题
【结束】
22
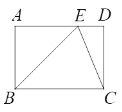
【题目】如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
(2)已知AB=1,∠ABE=45°,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com