
分析 (1)先提公因式x,转化为两个一元一次方程,再解方程即可;
(2)先移项,再提公因式,转化为两个一元一次方程,再解方程即可;
(3)先提公因式2,再提公因式x-3,转化为两个一元一次方程,再解方程即可;
(4)根据平方差公式,转化为两个一元一次方程,再解方程即可.
解答 解:(1)x(x-4)=0,
x=0或x-4=0,
∴x1=0,x2=4;
(2)x(x-$\frac{1}{2}$-1)=0,
x=0或x-$\frac{3}{2}$=0,
∴x1=0,x2=$\frac{3}{2}$;
(3)(x-3)(x-3+2)=0,
x-3=0或x-1=0,
∴x1=3,x2=1;
(4)[3(2x+3)+2(2x-5)][3(2x+3)-2(2x-5)]=0,
(10x-1)(2x+19)=0,
10x-1=0或2x+19=0,
∴x1=$\frac{1}{10}$,x2=-$\frac{19}{2}$.
点评 本题考查了用因式分解法解一元二次方程,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


科目:初中数学 来源: 题型:解答题
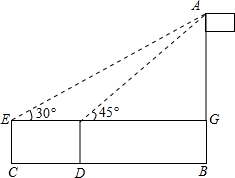 如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)
如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
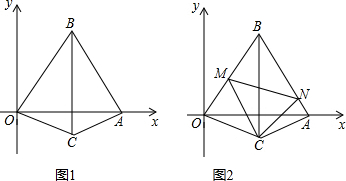
 如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.
如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com