
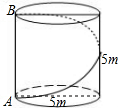
 壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?
壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?  长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
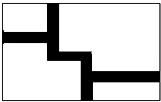 如图,在长为32 米,宽为20 米的矩形地面上修建同样宽度的道路(图中阴影部分),余下的部分种植草坪,要使草坪的面积为540m2,求道路的宽是多少米?
如图,在长为32 米,宽为20 米的矩形地面上修建同样宽度的道路(图中阴影部分),余下的部分种植草坪,要使草坪的面积为540m2,求道路的宽是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
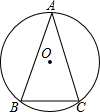 几何计算题:
几何计算题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | (a+2b)2=a2+2ab+b2 | C. | (a+b)2=a2+b2 | D. | (-a+b)2=a2-2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com