
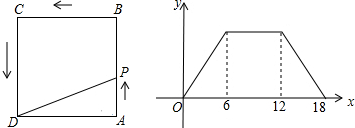
分析 (1)从图2中看到刚好6s时y最大,得到点P在AB上运动的时间,从而得到AB,x=17时,点P在CD边上,且PD=1即可;
(2)由图2面积没变的是中间一段,从而得到点P在BC上时,y值不变;
拓展:先判断点P在那段线段上运动,用三角形的面积公式计算即可;
探究:y是15时,得到点P在AB和CD这两段线段上,所以直接代入函数关系式中即可.
解答 解:(1)由图2,得到点P在AB上运动时间为6,
∵点P以1cm/s的速度运动,
∴AB=6÷1=6,
∵正方形ABCD,
∴AB=BC=CD=6,
当x=17(s)时,点P在线段CD上,PD=1,
∴y=$\frac{1}{2}$AD×PD=$\frac{1}{2}$×6×1=3,
故答案为6,3,
(2)∵△PAD的边AD时定值6,
∴点P到AD的距离不变时,△PAD的面积不变,
∴点P在BC上,
故答案为BC;
拓展:当0<x<6时,点P在线段AB上,PD=x,
∴y=$\frac{1}{2}$AD×PD=$\frac{1}{2}$×6×x=3x,
当12<x<18时,点P在线段CD上,PD=18-x,
∴y=$\frac{1}{2}$AD×PD=$\frac{1}{2}$×6×(18-x)=54-3x,
探究:∵y的值等于15cm2?
把y=15代入y=3x中,得15=3x,
∴x=5,
把y=15代入y=54-3x中,得15=54-3x,
∴x=13,
∴当x=5或13s时,y的值等于15.
点评 此题是四边形综合题,主要考查的是动点问题,解本题的关键是从图中找到对应的量,也是解本题的难点.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{x}^{2}}$+$\sqrt{{y}^{2}}$ | B. | $\sqrt{x-y}$=$\sqrt{x}$-$\sqrt{y}$ | C. | 5$\sqrt{7}$-3$\sqrt{5}$=2$\sqrt{2}$ | D. | 4$\sqrt{5}$-3$\sqrt{5}$=$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com