
【题目】(本小题满分18分)某校八(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |
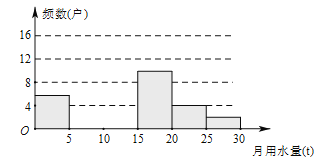
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
【答案】(1)12;0.08;图见解析;(2)68﹪;(3)120.
【解析】
试题(1)观察频数分布表,用16÷0.32或10÷0.20,先把频数总和求出来,然后用总和减去其它频数就是5<x≤10的频数,用4除以这个总和就是20<x≤25的频率(或者用1减去这些频率);根据频数对应补全频数分布直方图;(2)用水量不超过15吨的是前三组,把频率相加即为所求;(3)用1000户乘以用水量超过20 t的两组的频率和即是所求.
试题解析:(1)观察频数分布表,频数总和是:16÷0.32=50,5<x≤10的频数是:50-6-16-10-4-2=12,20<x≤25的频率是:4÷50=0.08,根据所求数值对应补全频数分布表和频数分布直方图;(2)用水量不超过15吨的是前三组,∴(0.12+0.24+0.32)×100﹪=68﹪.(3)用水量超过20 t的是后两组,∴1000×(0.04+0.08)=120(户).


科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球,羽毛球拍和乒乓球拍,已知篮球,羽毛球拍和乒乓球拍的单价比为8:3:2,且其单价和为130元,
(1)请问篮球,羽毛球拍和乒乓球拍的单价分别是多少元?
(2)若要求购买篮球,羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是乒乓球拍数量的4倍,且购买乒乓球拍的数量不超过15副请问有几种购买方案?哪种方案,才能使运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
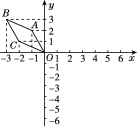
【题目】如图,在平面直角坐标系中,O,A,B,C的坐标分别为(0,0),(-1,2),(-3,3)和(-2,1).
(1)若图中的各个点的纵坐标不变,横坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.
(2)若图中的各个点的横坐标不变,纵坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点. 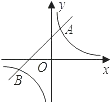
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F. 
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.
(1)求证:OE=OF;
(2)连结DE、BF,试说明四边形BFDE是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com