
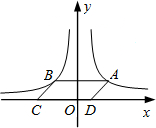
 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7.
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7. 分析 连结OA、OB,AB交y轴于E,由于AB⊥y轴,根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义得到S△OEA=$\frac{1}{2}$×3=1.5,S△OBE=$\frac{1}{2}$×4=2,则四边形ABCD为平行四边形,然后根据平行四边形的性质得到S平行四边形ABCD=2S△OAB=7.
解答 解:连结OA、OB,AB交y轴于E,如图,
∵AB∥x轴,
∴AB⊥y轴,
∴S△OEA=$\frac{1}{2}$×3=1.5,S△OBE=$\frac{1}{2}$×4=2,
∴S△OAB=1.5+2=3.5,
∵四边形ABCD为平行四边形,
∴S平行四边形ABCD=2S△OAB=7.
故答案为:7.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
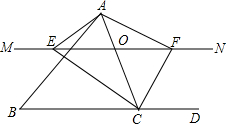 如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 大家知道在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
大家知道在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
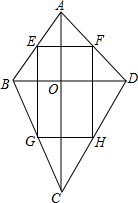 如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,
如图,四边形ABCD中,对角线AC⊥BD于点O,E、F、G、H分别是AB、AD、BC、CD的中点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com