
直线![]() 分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△COD,抛物线y=ax2+bx+c经过A、C、D三点.
分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△COD,抛物线y=ax2+bx+c经过A、C、D三点.
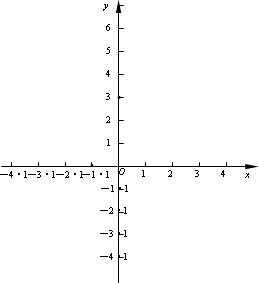
(1)写出点A、B、C、D的坐标;
(2)求经过A、C、D三点的抛物线表达式,并求抛物线顶点G的坐标;
(3)在直线BG上是否存在点Q,使得以点A、B、Q为顶点的三角形与△COD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
|
解:(1)A(3,0),B(0,1),C(0,3),D(-1,0) (4分) (2)∵抛物线 又∵抛物线经过A,C两点,∴ ∴ ∴ (3)解:过点G作GH⊥y轴垂足为点H, ∵
∴∠GBH=∠BAO (1分) ∵∠BAO+∠ABO=90°,∴∠GBH+∠ABO=90°,∴∠GBA=90°, ∴∠ABQ=∠DOC=∠AOB (1分) ①当 即 过点Q作QN⊥y轴,垂足为点N,设Q(x,y), ∵ ∵tan∠GBH= ②同理可得: |


科目:初中数学 来源: 题型:
 (2012•拱墅区一模)如图,在平面直角坐标系中,直线y=-x+1分别交x轴、y轴于A,B两点,点P(a,b)是反比例函数y=
(2012•拱墅区一模)如图,在平面直角坐标系中,直线y=-x+1分别交x轴、y轴于A,B两点,点P(a,b)是反比例函数y=| 1 |
| 2x |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
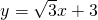 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市顺义区李桥中学九年级(上)第三次月考数学试卷(解析版) 题型:解答题
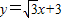 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
查看答案和解析>>
科目:初中数学 来源:2009年重庆市一中中考数学二模试卷(解析版) 题型:解答题
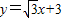 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.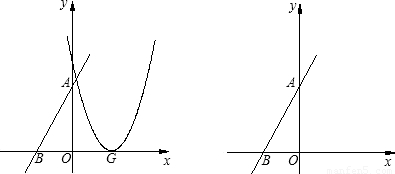
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(黑龙江黑河、齐齐哈尔、大兴安岭卷)数学(解析版) 题型:解答题
如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程 的两个根,点C在x轴负半轴上,
的两个根,点C在x轴负半轴上,
且AB:AC=1:2

(1)求A、C两点的坐标;
(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以 A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com