

���� ��1�������A��B�����꣬Ȼ�����ƽ���ı��ε����ʼ������C�����꣮
��2������������ֱ�������ã�
��3����B����B����ֱ��DE�ĶԳƵ㣬����OB�䣬����BB�佻ֱ��DE��F�����ֱ��DE�Ľ���ʽ���������ֱ��OB��Ľ���ʽ���Ӷ���B�䣨x��-$\frac{1}{2}$x����Ȼ����ݡ�FGE�ס�DOE���������B������꣬���ݴ���ϵ�������ֱ��B��C����ʽ���������̼������P�����꣬Ȼ�����PB��PC�ij��������������ܳ���ʽ������á�PBC�ܳ�����Сֵ��
��� �⣺��1����ֱ��y=2x+4��֪A��-2��0����B��0��4����
��OA=2��OB=4��
������ת��������OD=OB=4��
��AD=6��D��4��0����
���ı���ABCD��ƽ���ı��Σ�
��BC=AD=6��
��C��6��4����
�ʴ�Ϊ����6��4����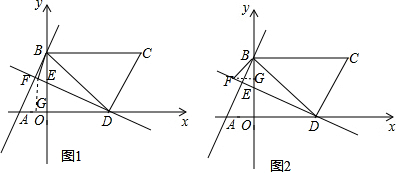
��2������BFD=90��ʱ����FG��x����G����ͼ1��
�ߡ�BFE=��DOE=90�㣬��BEF=��DEO��
���BEF�ס�DEO��
��$\frac{EF}{OE}$=$\frac{BE}{DE}$��
��OE=OA=2��OD=OB=4��OB=4��
��BE=4-2=2��DE=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$��
��$\frac{EF}{2}$=$\frac{2}{2\sqrt{5}}$��
��EF=$\frac{2\sqrt{5}}{5}$��
��DF=DE+EF=$\frac{12\sqrt{5}}{5}$��
��FG��OB��
���ODE�ס�GDF��
��$\frac{GF}{OE}$=$\frac{GD}{OD}$=$\frac{DF}{DE}$����$\frac{GF}{2}$=$\frac{GD}{4}$=$\frac{\frac{12\sqrt{5}}{5}}{2\sqrt{5}}$��
��GF=$\frac{12}{5}$��GD=$\frac{24}{5}$��
��OG=GD-OD=$\frac{4}{5}$��
��F��-$\frac{4}{5}$��$\frac{12}{5}$����
����FBD=90��ʱ����FG��y����G�����BFG=��CBD����ͼ2��
�ߡ�FGB=��EOD=90�㣬
���BFG�ס�DBO��
��$\frac{BG}{GF}$=$\frac{OD}{OB}$=$\frac{4}{4}$=1��
��BG=GF��
��BG=GF=x��
��OG=4-x��
��GE=4-x-2=2-x
��FG��AD��
���FGE�ס�DOE��
��$\frac{FG}{OD}$=$\frac{EG}{OE}$����$\frac{x}{4}$=$\frac{2-x}{2}$�����x=$\frac{4}{3}$��
��BG=GF=$\frac{4}{3}$��
��OG=4-$\frac{4}{3}$=$\frac{8}{3}$��
��F��-$\frac{4}{3}$��$\frac{8}{3}$����
��F���������-$\frac{4}{5}$��$\frac{12}{5}$����-$\frac{4}{3}$��$\frac{8}{3}$����
�ʴ�Ϊ��-$\frac{4}{5}$��$\frac{12}{5}$����-$\frac{4}{3}$��$\frac{8}{3}$����
��3����B����B����ֱ��DE�ĶԳƵ㣬����OB�䣬��ͼ3��
����BB�佻ֱ��DE��F��
��BF=B��F��
��BE=OE=2��
��EF��OB�䣬
��B��G��OA��G��
���OB��B=��EFB=90�㣬
���OBB��+��BOB��=90�㣬
�ߡ�BOB��+��GOB��=90�㣬
���GOB��=��OBB�䣬
���GOB��ס�B��BO��
��$\frac{B��G}{OB��}$=$\frac{OB��}{OB}$��
��D��4��0����E��0��2����
��ֱ��DE�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��ֱ��OB��Ľ���ʽΪy=-$\frac{1}{2}$x��
��B�䣨x��-$\frac{1}{2}$x����
��OB��=-$\frac{\sqrt{5}}{2}$x��
��$\frac{\frac{1}{2}x}{\frac{\sqrt{5}}{2}x}$=$\frac{\frac{\sqrt{5}}{2}x}{4}$�����x=-$\frac{8}{5}$��
��B�䣨-$\frac{8}{5}$��$\frac{4}{5}$����
��C��6��4����
��ֱ��B��C�Ľ���ʽΪy=$\frac{8}{19}$x+$\frac{28}{19}$��
��$\left\{\begin{array}{l}{y=\frac{8}{19}x+\frac{28}{19}}\\{y=-\frac{1}{2}x+2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{4}{7}}\\{y=\frac{12}{7}}\end{array}\right.$��
��P��$\frac{4}{7}$��$\frac{12}{7}$����
��B��0��4����C��6��4����
��PB=$\frac{4\sqrt{17}}{7}$��PC=$\frac{10\sqrt{17}}{7}$��
��BC=6��
���PBC�ܳ�����Сֵ=PB+PC+BC=2$\sqrt{17}$+6��
���� ������һ�κ������ۺ��⣬Ӧ�õ�֪ʶ���У�ֱ����������Ľ������꣬��ת�����ʣ����������Ƶ��ж������ʣ�����ϵ���������ʽ�����ɶ�����Ӧ�õȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
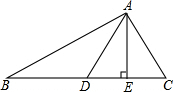 ��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ�AE��BC��E��AB=12��BC=10��AC=8����DE�ij���
��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ�AE��BC��E��AB=12��BC=10��AC=8����DE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֱ֪��y=$-\frac{3}{4}x+3$��ֱ��y=$kx-\frac{16}{3}$����x���ϵ�ͬһ����A��ֱ��y=$-\frac{3}{4}x+3$��y�ύ�ڵ�B��ֱ��y=$kx-\frac{16}{3}$��y��Ľ���ΪC��
��ֱ֪��y=$-\frac{3}{4}x+3$��ֱ��y=$kx-\frac{16}{3}$����x���ϵ�ͬһ����A��ֱ��y=$-\frac{3}{4}x+3$��y�ύ�ڵ�B��ֱ��y=$kx-\frac{16}{3}$��y��Ľ���ΪC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
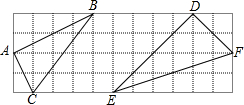 ��ͼ��ʾ������ֽ��ÿ��С�����εı߳�Ϊ1����ABC�͡�DEF�Ķ��㶼�ڷ���ֽ�ĸ���ϣ��жϡ�ABC�͡�DEF�Ƿ����ƣ���˵�����ɣ�
��ͼ��ʾ������ֽ��ÿ��С�����εı߳�Ϊ1����ABC�͡�DEF�Ķ��㶼�ڷ���ֽ�ĸ���ϣ��жϡ�ABC�͡�DEF�Ƿ����ƣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2�� | B�� | ��-2��0�� | C�� | ��4��0�� | D�� | ��0��-2�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com